Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 28

Uma esfera de plástico de 4   m m de diâmetro, cuja densidade é 1150   k g / m 3 , é jogada na água a 20 ° C . Determine a velocidade terminal da esfera na água.

Passo 1

Temos a seguinte situação:

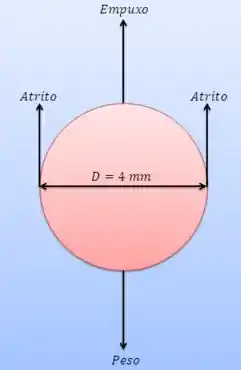
Uma esfera de diâmetro D = 4 × 10 - 3   m é solta na água. Devemos obter a velocidade terminal da esfera. Vamos lá?

Para começar, vamos fazer um balanço de forças:

F p - F e - F D = F r e s

Como queremos a velocidade terminal, estamos em uma situação de equilíbrio. Ou seja:

F r e s = 0

Então:

F p - F e - F D = 0

F D = F p - F e

Passo 2

Antes de continuar, vamos encontrar as propriedades da água a 20 ° C . Pela Tabela A - 3 do apêndice:

ρ f = 998   k g / m 3

μ = 1,002 × 10 - 3   m 2 / s

Voltando para a equação, vamos reescrever as forças como:

F D = C D A p ρ f V t 2 2

F p = ρ e s f × g × v o l u m e

F e = ρ f × g × v o l u m e

Então:

C D A p ρ f V t 2 2 = ρ e s f × g × v o l u m e - ρ f × g × v o l u m e

C D A p ρ f V t 2 2 = ρ e s f - ρ f × g × v o l u m e

V t 2 = 2 × ρ e s f - ρ f × g × v o l u m e C D A p ρ f

Passo 3

Para prosseguir, precisamos do coeficiente de atrito. Considerando que estamos em regime laminar podemos dizer que:

C D = 24 R e

C D = 24 μ ρ f V t D

Para uma esfera também podemos dizer que:

v o l u m e = π D 3 6

A p = π D 2 4

Voltando para a relação de velocidade terminal:

V t 2 = 2 × ρ e s f - ρ f × g × π D 3 6 24 μ ρ f V t D × π D 2 4 × ρ f

V t 2 = 2 × ρ e s f - ρ f × g × 4 × D 6 × V t × D 24 μ

V t = ρ e s f - ρ f × g × D 2 18 μ

V t = 1150 - 998 × 9,81 × 4 × 10 - 3 2 18 × 1,002 × 10 - 3 = 1,3   m / s

Resposta

Velocidade terminal V t = 1,3   m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que são usados os flaps nos bordos de ataque e de fuga das asas de grandes aviões durante a decolagem e o pouso? Um avião pode decolar ou pousar sem eles?
Como os flaps afetam a sustentação e o arrasto das asas?
O ar está escoando por um aerofólio simétrico com um ângulo de ataque de 5°. (a) A sustentação e (b) o arrasto, que agem sobre o aerofólio, serão iguais a zero ou não?
O que é estol? O que faz um aerofólio entrar em estol? Por que os aviões comerciais não podem voar em condições próximas de estol?
Considere um avião, que decola a 190 km/h com sua carga total. Se o peso do avião for aumentado em 20 por cento em razão de uma sobrecarga, determine a velocidade na qual o avião sobrecarregado irá de