Uma turbina de impulsão deve desenvolver 15 MW com roda única, em um local onde a altura de carga líquida é 350 m. Determine a velocidade, o diâmetro do rotor e o diâmetro do jato apropriado para operação com jato único e com jatos múltiplos. Compare com uma instalação de dois rotores em série. Estime o consumo de água requerido.
Passo 1
Tá legal! Vamos começar esse exercíico considerando um caso ideal, onde temos eficiência máxima, então através da figura 10.36, temos:
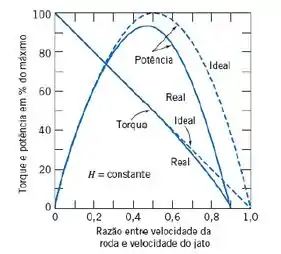
E, agora, da figura a seguir, de novo, adotando o caso de máxima eficiência para turbina de impulsão, temos:
E temos que a eficiência máxima é:
Passo 2
Agora vamos calcular a velocidade do jato, que pode ser encontrada através de:
Substituindo os valores conhecidos:
Através da relação entre e vista no passo 1, temos:
Agora, o consumo de água pode ser encontrado através da relação da potência útil produzida pelo sistema:
Então, substituindo os valores conhecidos, temos:
Passo 3
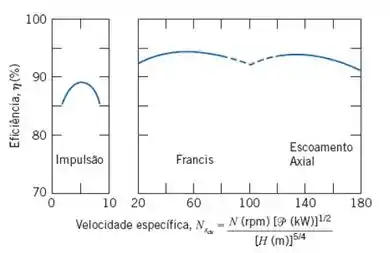
Agora vamos escrever a velocidade específica do sistema, no entanto, a velocidade específica precisa ser convertida para com as unidades em kW, rpm e m. Então, conforme vimos nessa seção, a conversão será:
Substituindo o valor de extraído do diagrama do passo 1, temos:
E a velocidade específica pode ser escrita como:
Então, isolando a rotação dessa equação, chegamos em:
Substituindo os valores conhecidos, temos que a rotação para um único jato será:
Agora, calculando o diâmetro do jato através da vazão, temos:
Substituindo os valores conhecidos:
E, para encontrar o diâmetro do rotor, temos que encontrar primeiro o raio do rotor através da seguinte equação:
Substituindo os valores conhecidos:
Então o diâmetro do rotor será:
Passo 4
Agora, para analisar o caso onde temos vários jatos, nós vamos analisar a potência e a vazão por jato, então, da equação da velocidade angular, temos:
Como a potência está associada ao número de jatos, temos que:
Então, substituindo essa expressão na equação anterior, temos:
Então, podemos ver que essa equação tem o mesmo formato da equação para um único jato, com exceção do termo multiplicando, então, a relação entre a velocidade para um único jato e vários jatos pode ser escrita como:
Agora, analisando da mesma forma a equação para o diâmetro do jato, temos:
Nesse caso, estamos analisando a vazão por jato, então temos:
Substituindo essa expressão na equação anterior:
Podemos ver que essa equação é a mesma usada para o jato único, com exceção do termo dividindo, então, podemos relacionar o diâmetro de um único jato com vários jatos através de:
Agora, por último, para o diâmetro do rotor, temos:
Como vimos que a velocidade angular depende diretamente de , nesse caso, como temos no denominador, podemos escrever o diâmetro do rotor para vários jatos como:
Passo 5
Agora então, vamos substituir diferentes valores de para as relações encontradas no passo 4, então, para , temos:
Para :
Para :
Uma instalação com 2 rotores em série é equivalente a um rotor com dois jatos.