Projete um sistema de tubulação para o fornecimento da água de uma turbina, a partir de um reservatório na montanha. O reservatório está localizado a 320 m acima do local da turbina. A eficiência da turbina é 83%, e ela deve produzir 30 kW de potência mecânica. Defina o mínimo tamanho padrão requerido para o tubo de suprimento de água para a turbina e a vazão volumétrica de água requerida. Discuta os efeitos de eficiência da turbina, rugosidade do tubo e instalação de um difusor na saída da turbina sobre o desempenho da instalação.
Passo 1
Tá legal! Vamos começar esse exercício escrevendo a perda de carga para o sistema, pois é a partir dela que vamos encontrar o diâmetro da tubulação, então, temos:
Conforme vimos no exemplo 10.14 dessa seção, a perda de carga para o sistema na potência máxima é dada por:
E, de acordo com a figura 10.40 a seguir, vamos adotar e para realizar nossos cálculos.
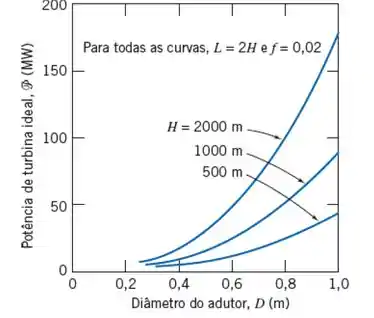
Então, substituindo os valores de e na equação para a perda de carga, temos:
E, isolando a velocidade nessa expressão, temos:
Passo 2
Agora, sabemos que a vazão do sistema pode ser escrita como:
E que a potência hidráulica disponível é:
E, por sua vez, a potência mecânica produzida será:
Substituindo a expressão para a potência hidráulica nessa última equação, temos:
Agora vamos substituir a expressão para a vazão nessa equação:
E, por fim, vamos substituir a expressão encontrada para a velocidade no passo 1, então, a equação se torna:
Passo 3
Agora como temos a equação da potência mecânica em função do diâmetro e de outros parâmetros conhecidos, vamos substituir os valores conhecidos, ficando com:
Então nós vamos plotar esse gráfico e verificar para qual diâmetro o sistema atende à potência mecânica de 30 kW. O gráfico dessa função será:
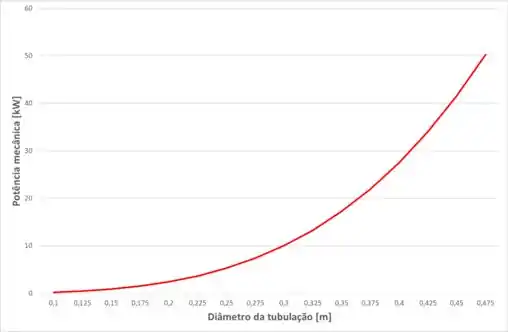
Então, a partir do gráfico, podemos ver que a potência de 30 kW será atingida para um diâmetro de tubulação de: