Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 8º - Capítulo 1.Problemas - Ex. 83

Use Eq. (1.39) to fi nd and sketch the streamlines of the

following flow fi eld:

u 5 K(x2 2 y2); v 5 22Kxy; w 5 0, where K is a constant.

Hint: This is a first-order exact differential equation.

Passo 1

Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊

O comportamento da linha de fluxo é dada pela equação abaixo

d x u = d y v = d z w

Aqui, u é a velocidade na direção x , v é a velocidade na direção y e w é a velocidade na direção z

Passo 2

Substituindo k x 2 - y 2 para u , - 2 k x y para v e 0 para w na equação

d x k x 2 - y 2 = - d y 2 k x y = 0

→ 2 x y d x + x 2 - y 2 d y = 0

Passo 3

Essa equação é uma equação diferencial de primeira ordem exata e a solução é obtida substituindo g y para x

x = g y

Aqui, g é uma variável

Diferenciando essa última equação de ambos os lados

d x = y d g + g d y

Substituindo essa equação na primeira

2 g y 2 y d g + g d y + y 2 g 2 - 1 d y = 0

Dividindo essa equação por y 2

2 g y d g + g d y + g 2 - 1 d y = 0

→ 2 g d g 1 - 3 g 2 = d y y

Passo 4

Integrando essa última equação em ambos os lados

- 1 3 ln ⁡ 1 - 3 g 2 = ln ⁡ y + C

→ ln ⁡ 103 g 2 - 1 / 3 = ln ⁡ y + C

Substituindo g = x / y

ln ⁡ 1 - 3 x 2 y 2 - 1 / 3 = ln ⁡ y + C

→ ln ⁡ y 3 ⋅ y 2 - 3 x 2 y 2 = 3 C

→ y 3 - 3 x 2 y = e 3 C

Passo 5

Essa é uma equação cúbica e pode ser considerada como a possibilidade para um comportamento de curva.

Considerando a seguinte tabela para diferentes valores de y

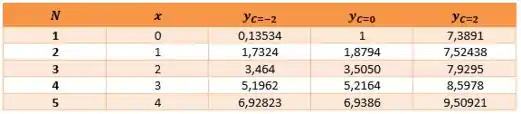
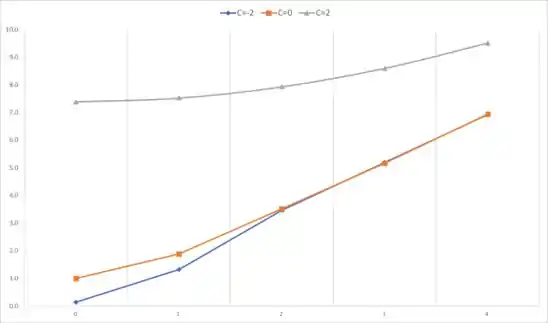
Resposta

Resposta nos passos.

Exercícios de Livros Relacionados

Suppose we know little about the strength of materials butare told that the bending stress σ in a beam is proportionalto the beam half-thickness y and also depends on thebending moment M and the beam
Air, assumed to be an ideal gas with k 5 1.40, flows isentropically through a nozzle. At section 1, conditions are sealevel standard (see Table A.6). At section 2, the temperature is 2508C. Estimate (
Books on porous media and atomization claim that the viscosity µ and surface tension Y of a fluid can be combinedwith a characteristic velocity U to form an important dimensionless parameter. (a) Veri
The Ekman number, Ek, arises in geophysical fluiddynamics. It is a dimensionless parameter combining seawater density ρ, a characteristic length L, seawaterviscosity µ, and the Coriolis frequency Ω si
A tank contains 9 kg of CO2 at 208C and 2.0 MPa. Estimatethe volume of the tank, in m3