Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 4.Problemas - Ex. 148
Varas longas de madeira 18 cm de diâmetro são expostas ao ar a 30°C com um coeficiente de transferência de calor de . Se a temperatura central da barra for medida em 15°C após um período de 3 horas, a temperatura inicial da barra será:
a) 11,9°C;
b) 4,9°C;
c) 1,7°C
d) 0°C;
e) -9,2°C.
Passo 1
Vamoo que vamooo!!
Primeiro, nós queremos achar o que?
A temperatura inicial das barras, certo?
Mas antes de qualquer coisa precisamos saber o número de Biot, para a haste A:
Sabemos que:
Agora é só calcular o Biot:
Como o nós não podemos fazer a análise do sistema agrupado.
E agora?
Simples!! Nós podemos usar outra equação para a barra:
Então nós vamos precisar achar e
Passo 2
Olhando a Tabela:
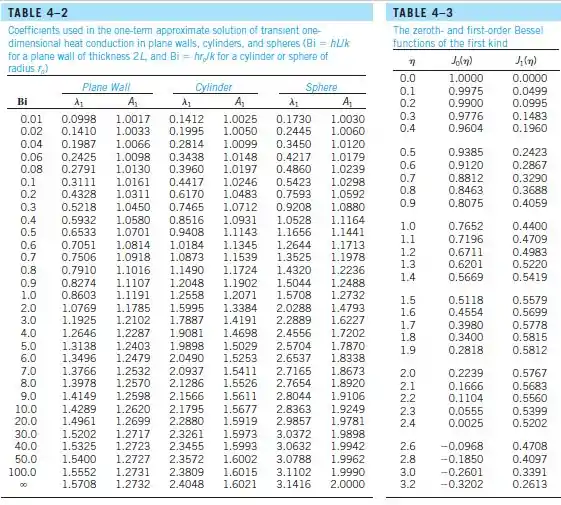
Pela tabela nós achamos que:
Agora que temos a fórmula nós só precisamos ver quais dados nós temos, não é?
Quando estamos falando da temperatura central:
Agora é só achar o tempo adimensional
Se:
Substituindo:
Passo 3
Colocando tudo na fórmula do Passo 1:
A única coisa que ainda não temos é , certo? Mas a tabela nos dá o seu valor:
Substituindo:
Por isso, a temperatura inicial deve ser de
Então a resposta deverá ser a letra (b) !!
Bem legal, não foi??