Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 60

Um longo bastão cilíndrico, com 60 mm de diâmetro e propriedades termofísicas iguais a ρ = 8000 kg/m3, c = 500 J/(kg · K) e k = 50 W/(m ·K), encontra-se inicialmente a uma temperatura uniforme e é aquecido em um forno de convecção forçada mantido a 750 K. O coeficiente de transferência de calor por convecção é estimado igual a 1000 W/(m2 · K).

(a) Qual é a temperatura no eixo central do bastão quando a sua temperatura na superfície é de 550 K?

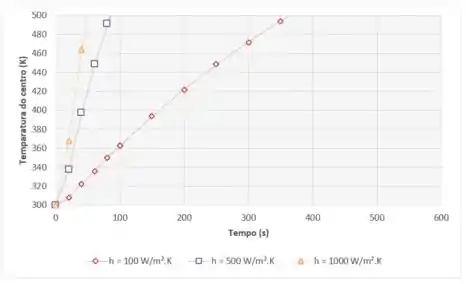
(b) Em um processo de tratamento térmico, a temperatura no eixo central do bastão deve ser aumentada de Ti = 300 K a T = 500 K. Calcule e represente graficamente os históricos de temperatura no eixo central do bastão para h = 100, 500 e 1000 W/(m2 · K). Em cada caso, o cálculo pode ser interrompido quando T = 500 K.

Passo 1

Vamos analisar o enunciado juntos e entender o que o problema quer de você.

Temos um bastão cilíndrico que é aquecido em um forno de convecção forçada.

Em primeiro lugar, devemos encontrar a temperatura do eixo central no momento em que a temperatura da superfície é T S = 550   K   .

Para isso, se a gente supor tempos muito longos ( F o > 0,2 ) podemos modelar a temperatura adimensional na superfície ( r * = R R = 1 ) a partir da equação:

ϴ S * = T S - T ∞ T i - T ∞ = ϴ 0 * J 0 ( ζ 1 r * )

Depois, podemos calcular a temperatura ϴ 0 * , que é no eixo central do bastão ( r * = 0 ):

ϴ 0 * = T 0 - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o )

Sendo   C 1 e ζ 1 coeficientes que podem ser calculados a partir da Tabela 5.1, F o o adimensional Número de Fourier, T S a temperatura na superfície do bastão, T 0 a temperatura em r * = 0 , T i a temperatura inicial e T ∞ a temperatura do ar.

Então, para calcular a temperatura do eixo central para uma temperatura de superfície conhecida em determinado momento, podemos fazer:

T S - T ∞ T i - T ∞ = ϴ 0 * J 0 ζ 1 r * → T S - T ∞ T i - T ∞ = T 0 - T ∞ T i - T ∞ J 0 ζ 1 r * → T 0 = T ∞ + T S - T ∞ J 0 ζ 1 r *

Depois, no final da questão, devemos colocar a temperatura do eixo central em função do tempo para diferentes valores de coeficiente de convecção h .

Agora, pra gente não se perder, vamos guardar as propriedades que vamos usar nos próximos passos:

T S = 550   K   e   T ∞ =   750   K R = 60   m m 2 = 30   m m = 0,03   m   k = 50 W m . K , ρ   =   8000 k g m 3 , c   =   500 J k g   ·   K         α   =   k ρ c = 1,25   x 10 - 5 m 2 s h   =   1000 W m ²   ·   K

Passo 2

Primeiro, devemos calcular o número de Biot para o problema:

B i =   h L k =   1000 W m ²   ·   K 0,03   m   50   W m . K =   0,6  

Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 para o cilindro, olhando para o valor de de B i = 0,6 :

B i   = 0,6 →   ζ 1 = 1,0184     C 1 =   1,1345

Utilizando a equação deduzida no Passo 1:

T 0 = T ∞ + T S - T ∞ J 0 ζ 1 r * = 750   K + 550   K - 750   K J 0 1,0184 1 = 750   K + - 200   K J 0 1,0184

A função J 0 é a Função de Bessel de Ordem Zero, na Tabela B.4 (página 652). Como não temos J 0 1,0184 , vamos interpolar os valores de J 0 1,0 e J 0 1,1 :

  J 0 1,0 = 0,7652 J 0 1,1 = 0,7196 → J 0 1,0184 = 0,7568

Sendo assim:

T 0 = 750   K + - 200   K 0,7568 = 485,73   K

Passo 3

Pra finalizar a questão, vamos resolver a letra (b).

Primeiro, devemos deixar o número de Fourier em função do tempo t :

F o = α t L ² =     1,25   x 10 - 5 m 2 s t ( 0,03   m ) ² = 0,014 t

Agora, vamos encontrar expressões para temperatura ao longo do tempo para cada uma das seguintes condições de coeficiente de convecção h :

  • Para h = 1000 W m 2 . K

    • T 0 - T ∞ T i - T ∞ =   C 1 e x p ⁡ ( - ζ 1 ² F o ) → T 0 ( t ) = 750 + ( 300 - 750 ) ( 1,1345 ) e x p ⁡ ( - ( 1,0184 ) ² 0,014 t )

    → T 0 ( t ) = 750 - ( 510,53 ) e x p ⁡ ( - 0,01452 t )

  • Para h = 100 W m 2 . K

    • Vamos calcular o número de Biot:

    B i =   h L k =   100 W m ²   ·   K 0,03   m   50   W m . K =   0,06  

    Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 para o cilindro, para o valor de de B i = 0,06 .

    B i   = 0,06 →   ζ 1 = 0,3438     C 1 =   1,0148

    Agora, vamos encontrar T 0 ( t ) :

    T 0 ( t ) = 750 + ( 300 - 750 ) ( 1,0148 ) e x p ⁡ ( - ( 0,3438 ) ² 0,014 t )

    → T 0 t = 750 - ( 456,67 ) e x p ⁡ ( - 0,001655 t )

  • Para h = 500 W m 2 . K

Vamos calcular o número de Biot:

B i =   h L k =   500 W m ²   ·   K 0,03   m   50   W m . K =   0,3  

Vamos agora na Tabela 5.1 para calcular os valores dos coeficientes de   C 1 e ζ 1 para o cilindro, para o valor de de B i = 0,3 .

B i   = 0,3 →   ζ 1 = 0,7465     C 1 =     1,0712

Agora, vamos encontrar T 0 ( t ) :

T 0 ( t ) = 750 + ( 300 - 750 ) ( 1,0712 ) e x p ⁡ ( - ( 0,7465 ) ² 0,014 t )

→ T 0 ( t ) = 750 - ( 482,04 ) e x p ⁡ ( - 0,0078 t )

Pra matar de vez essa questão vamos agora traçar o gráfico de temperatura no centro por tempo com ajuda do Excel:

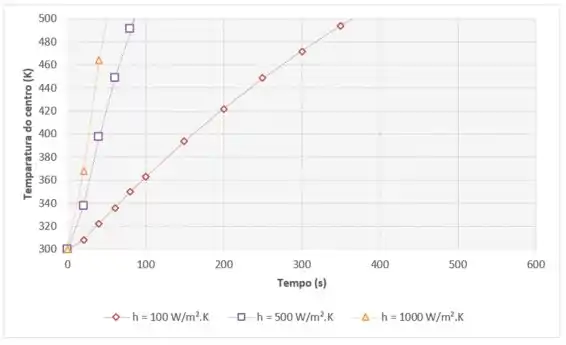
Como é possível ver pelo gráfico, quanto maior o coeficiente de convecção h , menor a resistência à transferência de calor, e mais rápido a temperatura no centro do bastão alcança 500 K.

UFAAAAAAAA! Agora a gente pode respirar!

Resposta

(a) a temperatura no eixo central do bastão quando a sua temperatura na superfície é de 550 K é T 0 = 485,73   K .

(b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas esferas, A e B , inicialmente a 800K , são subitamente submersas em grandes banhos, que são mantidos à mesma temperatura constante de 320K . Os parâmetros a seguir estão associados a cada uma das
Em um processo de fabricação, longos bastões de diferentes diâmetros estão a uma temperatura uniforme de 400°C no interior de um forno de cura, do qual são retirados e resfriados por convecção forçada
A massa específica e o calor específico de um determinado material são conhecidos ( ρ=1200k g / m 3 ,c p = 1250J / ( k g·K ) ) , mas a sua condutividade térmica é desconhecida. Para determinar a condu
Bilhas de aço inoxidável (AISI 304), que foram aquecidas uniformemente até 850°C, são endurecidas pelo resfriamento em um banho de óleo mantido a 40°C. O diâmetro de cada esfera é de 20 mm e o coefici
Uma esfera de vidro cal-soda de diâmetro D 1=25m m é encapsulada em uma casca esférica de baquelita de espessura L=10m m . A esfera composta está inicialmente a uma temperatura uniforme, T i = 40 ° C