A variação da viscosidade do ar com a temperatura é bem correlacionada pela equação empírica de Sutherland

Os valores de e que melhor ajustam essa equação são dados no Apêndice A para serem usados em unidades do Sistema Internacional. Use esses valores para desenvolver uma equação para calcular a viscosidade do ar em unidades do Sistema Gravitacional Britânico como uma função da temperatura absoluta em graus Rankine. Verifique a exatidão dos seus resultados comparando-os com os dados do Apêndice A.

Agora precisamos converter essas unidades para o sistema britânico, então, temos:

Tá legal, agora precisamos pegar uma temperatura na tabela A.8 do apêndice A e conferir nossas constantes obtidas no passo 2, então, temos:

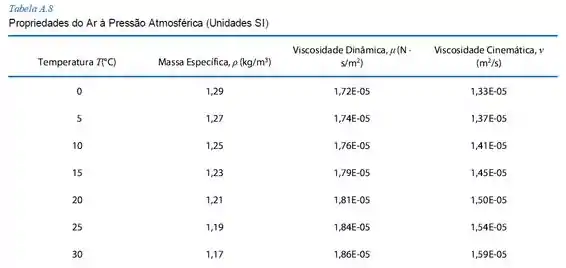
Para a temperatura de:

Então, calculando com os valores obtidos para o nosso sistema, temos:

Então, substituindo os valores na equação de Sutherland, temos:

Convertendo esse valor para as unidades do sistema internacional para verificar o valor, obtido, temos:

Então, o valor obtido é o mesmo fornecido na tabela A.8 do Apêndice A, dessa forma, fizemos a conversão da equação corretamente.