Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas Abrangentes - Ex. 7

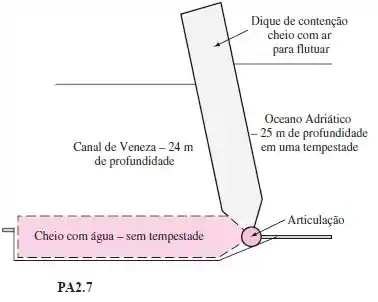
Veneza, na Itália, está afundando lentamente, de maneira que agora, especialmente no inverno, as praças e calçadas ficam inundadas durante as tempestades. A solução proposta é o dique flutuante da Figura P A 2.7 . Quando cheio com ar, ele se levanta e bloqueia o mar. O dique tem 30   m de altura, 5   m de largura e 20   m de profundidade. Considere uma massa específica uniforme de 300   k g / m 3 quando flutuando. Para a diferença mostrada de 1   m entre o mar e a laguna, calcule o ângulo com o qual o dique flutua.

Passo 1

E aí, tudo bem? Bora resolver mais essa comigo!

Primeiro vamos montar um esqueminha para o dique apresentado!

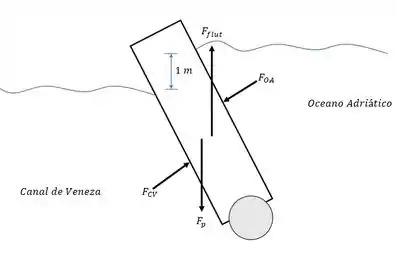
Vamos Considerar que ρ m a r = 1025   k g m 3 .

Lembrando que θ é o ângulo de inclinação do dique.

Agora vamos organizar nossos dados:

Do lado do Oceano o lado submerso será, L O A = 25 cos ⁡ θ , da mesma forma para o canal. L O A = 24 cos ⁡ θ , para a flutuabilidade L f l u t = 24 + 25 2 = 24,5 .

Agora que temos nossos comprimentos vamos organizar as forças por unidade de comprimento:

F O A = ρ g h O A L O A = 1025 k g m 3 ⋅ 9,81 m s 2 ⋅ 25   m 2 ⋅ 25 m cos ⁡ θ

F O A = 3,142 ⋅ 10 6   N / m cos ⁡ θ

F C V = ρ g h C V L C V = 1025 k g m 3 ⋅ 9,81 m s 2 ⋅ 24   m 2 ⋅ 24 m cos ⁡ θ

F C V = 2,896 ⋅ 10 6   N / m cos ⁡ θ

F P = ρ d g h d L d = 300 k g m 3 ⋅ 9,81 m s 2 ⋅ 30 ⋅ 5 m 2

F p = 441.450   N / m

F f l u t = ρ g h d L f l u t = 1025 k g m 3 ⋅ 9,81 m s 2 ⋅ 24,5 ⋅ 5 m 2

F f l u t = 1,232 ⋅ 10 6   N m

Passo 2

Agora vamos fazer a somatória de momentos, para encontrar o ângulo de inclinação do nosso dique, assim:

Σ M d = F O A ⋅ L O A 3 + F p ⋅ L ⋅ sen ⁡ θ 2 - F C V L C V 3 - F f l u t L f l u t ⋅ sen ⁡ θ 2 = 0

Substituindo:

6,62 2 ⋅ 10 6 ⋅ sen ⁡ θ + 2 6,183 ⋅ 10 6 cos 2 ⁡ θ - 23,168 ⋅ 10 6 cos 2 ⁡ θ - 15,092 ⋅ 10 6   sen ⁡ θ

Com o auxilio de um software, chegamos à:

θ ≈ 26,3 °

Isso é tudo pessoal, conseguimos mais uma! \o/

Resposta

θ ≈ 26,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cilindro de ferro fundido, de 30c m de diâmetro e 30c m de altura, é imerso em água do mar ( γ = 10300N / m 3 ) . Qual é o empuxo que a água exerce no cilindro? Qual seria o empuxo se o cilindro fo
Um cilindro que pesa 500N e cujo diâmetro é 1m flutua na água ( γ = 10000N / m 3 ) , com seu eixo na vertical, como mostra a figura. A âncora consiste de 0,23m 3 de concreto de peso específico 25000N
A comporta de perfil A B , articulada em A e de largura 1m , possui uma bóia esférica de diâmetro D = 2m e peso G = 6000N . Sabendo que a comporta se abre quando o nível da água atinge o ponto A , con
Um corpo pesa 800N no ar e, quando imerso em água ( γ = 10000N / m 3 ) , tem um peso aparente de 500N . Determinar o volume do corpo e seu peso específico. Observação: peso aparente é o peso do corpo
A solid wooden cone (SG = 0.729) fl oats in water. Thecone is 30 cm high, its vertex angle is 908, and it floats withvertex down. How much of the cone protrudes above thewater?