Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 2
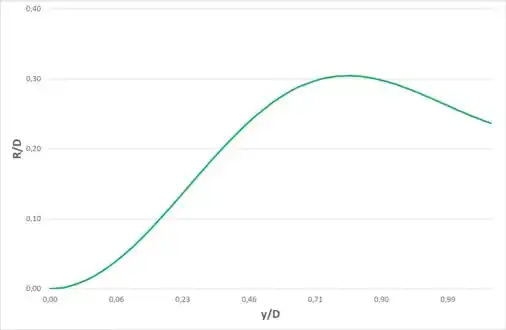
Verifique a equação dada na Tabela 11.1 para o raio hidráulico de um canal circular. Avalie e trace o gráfico da taxa , para profundidade de líquido entre 0 e D.
Passo 1
Tá legal! O canal circular é dado por:
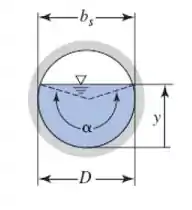
Então vamos começar encontrando a equação para a área do canal, que pode ser encontrada dividindo a área em em uma seção circular e mais dois triângulos, então, temos:
Sabemos que existe uma identidade trigonométrica dada por:
E, no nosso caso, temos:
Então, substituindo a identidade e o valor de , chegamos em:
Sabemos também que:
Então, substituindo essa expressão na equação para a área, temos:
Que é a equação na tabela 11.1
Passo 2
Agora para encontrar o perímetro molhado, basta que encontremos o comprimento do arco de circunferência com abertura , então:
Que é a mesma fórmula fornecida na tabela 11.1.
Passo 3
Agora, para encontrar uma relação para o raio hidráulico, devemos fazer:
Substituindo os valores conhecidos, temos:
E, estamos no caminho certo, pois essa é a equação fornecida na tabela 11.1.
Passo 4
Agora, para plotar o gráfico de em função da altura , devemos dividir a equação de encontrada no passo 3 por , então, temos:
Agora, sabemos que o nível de água é dado pela geometria do canal mostrado no passo 1, então temos:
E a profundidade em relação à será:
E dessa forma, gráfico de para a profundidade indo de 0 a será:
