Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 3.Problemas - Ex. 24

Uma veste protetora para bombeiros, identificada como um turnout coat, é tipicamente construída com um conjunto de três camadas separadas por espaços de ar, como mostrado esquematicamente.

Dimensões representativas e condutividades térmicas das camadas são apresentadas a seguir.

Os espaços de ar entre as camadas têm 1 mm de espessura e o calor é transferido nesta região por condução e por troca radiante através do ar estagnado. O coeficiente radiante linearizado para um espaço pode ser aproximado por hrad = σ (T1 + T2) ( T1²+ T2²) ≈ 4σTmed³ , na qual Tmed representa a temperatura média das superfícies limites do espaço. Deste modo, o fluxo radiante através do espaço pode ser representado por q’’rad = hrad = (T1 – T2).

  1. Represente o turnout coat por um circuito térmico, identificando todas as resistências térmicas. Calcule e coloque em uma tabela as resistências térmicas por unidade de área (m2 · K/W) para cada uma das camadas, assim como para os processos de condução e radiação nos espaços de ar. Admita que um valor de Tmed = 470 K possa ser usado para aproximar a resistência radiante em ambos os espaços. Comente sobre a magnitude relativa das resistências.
  2. Para um ambiente típico de fogo no qual bombeiros frequentemente trabalham, o fluxo térmico radiante típico no lado do fogo do turnout coat é de 0,25 W/cm2. Qual é a temperatura da superfície externa do turnout coat se a temperatura da superfície interna for de 66°C, uma condição que poderia resultar em uma queimadura?

Passo 1

Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.

Vamos olhar o esquema ilustrativo abaixo, que demonstra os mecanismos de transferência de calor que estão agindo no nosso sistema:

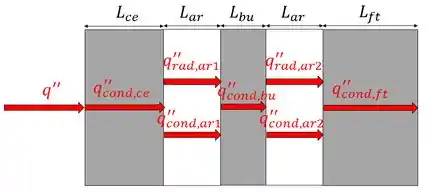
Como é possível notar, na camada externa (ce), na barreira de umidade (bu) e no forro térmico (ft) temos apenas transferência de calor condutiva e nos espaços de ar temos transferência de calor tanto condutiva quanto por radiação.

Para resolver esse problema a gente tem que encontrar a resistência térmica total da parede depois de esboçar o circuito térmico associado ao volume de controle que vamos analisar.

Além disso, a gente tem que calcular a temperatura da superfície externa do turnout coat.

Antes de ir para os próximos passos, vou deixar aqui com vocês algumas propriedades que vamos utilizar nos próximos passos:

L c e = 0,8   m m = 0,0008   m ;   k c e = 0,047 W m . K L a r = 1   m m = 0,001   m ;   k a r T a b e l a   A . 4 , p á g i n a   634 = 0,0387 W m . K ( p a r a   o   a r   a   473   K ) L b u = 0,55   m m = 0,00055   m ;   k b u = 0,012 W m . K L f t = 3 , 5   m m = 0,003 5   m ;   k f t = 0,038 W m . K T m e d   =   470   K   ,   T i   = 66 ° C =   339   K   q ' ' = 0,25 W c m 2 = 2500 W m ²

Passo 2

Primeiro, vamos resolver o item (a).

Olhando para o esquema apresentado na imagem do Passo 1, podemos expressar o circuito térmico para o problema com o esquema ilustrativo abaixo:

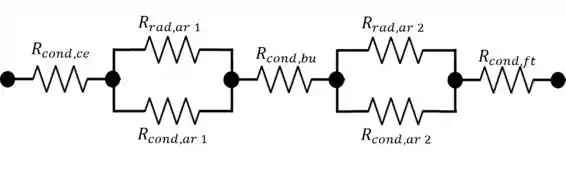
Pela imagem, devemos calcular duas resistências equivalentes em paralelo entre as camadas de ar:

1 R e q ,   a r   1 = 1 R c o n d , a r   1 + 1 R r a d , a r   1

1 R e q ,   a r   2 = 1 R c o n d , a r   2 + 1 R r a d , a r   2

Mas antes, vamos calcular cada uma das resistências individuais:

R c o n d , c e = L c e k c e = 0,00 0 8   m 0,047 W m . K = 0,017   m ² K / W

R c o n d , a r   1 = R c o n d , a r   2 = L a r k a r = 0,001   m 0,0387 W m . K = 0,026   m ² K / W

R r a d , a r   1 = R r a d , a r   1 = 1 h r a d = 1 4 σ T m e d 3 = 1 4 5,67 x 10 - 8 W m ² K 4 ( 470   K ) 3 = 0,042   m 2 K / W

R c o n d , b u = L b u k b u = 0,00055   m 0,012 W m . K = 0,046   m ² K / W

R c o n d , f t = L f t k f t = 0,0035   m 0,038 W m . K = 0,092   m ² K / W

Vamos calcular as duas resistências equivalentes em paralelo:

1 R e q ,   a r   1 = 1 0,026   m ² K / W + 1 0,042   m 2 K / W   → R e q ,   a r   1 = 0,016   m ² K / W

1 R e q ,   a r   2 = 1 0,026   m ² K / W + 1 0,042   m 2 K / W   → R e q ,   a r   2 = 0,016   m ² K / W

Ao comparar-se as magnitudes das resistências, pode perceber que todas foram muito próximas, na ordem de 10 - 2 .

Agora, devemos calcular a resistência total equivalente do circuito:

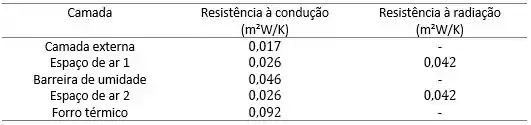
R t o t =   R c o n d , c e + R e q ,   a r   1 + R c o n d , b u + R e q ,   a r   2 + R c o n d , f t → R t o t = 0,187   m 2 K / W

A tabela com as resistências estará apresentada no item Resposta.

Passo 3

Pra finalizar a questão, vamos resolver o item (b).

Queremos encontrar a temperatura da superfície externa da turnout coat. Para isso, vamos utilizar a seguinte equação:

q ' ' =   T e - T i R t o t

Reorganizando e substituindo as propriedades que o enunciado já deu e a resistência que calculamos no Passo 1:

T e =   T i + q ' ' R t o t = 339   K + 2500 W m ²   0,187 m 2 K W = 806,5   K

Resposta

(a)

(b)   T e = 806,5   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dissipador de calor de alumínio ( k = 230W / m ⋅ K ), usado para resfriar uma matriz de chips eletrônicos, consiste em um canal quadrado de largura interna w = 30m m , através do qual o fluxo de lí
Considere a água do Exemplo 1.5 como sendo inicialmente líquida em sua temperatura de fusão. A superfície da parede externa é repentinamente reduzida para T 1 = - 30 ° C , resultando na solidificação
Considere uma área de composta de altura total H = 20m m e espessura L = 30m m . A seção A tem espessura L A = 10m m , e as seções B e C cada uma tem altura H B = 10m m e espessura L B = 20m m . As te
24 – Duas paredes espessas são separadas por uma lacuna de vácuo de espessura L. Um cilindro de diâmetro D, passa entre as paredes. Todas as superfícies são altamente polidas (suas emissividades são m
10 - A sensação de calafrio (resfriamento pelo vento), que é experimentada em dias frios com vento, está relacionada ao aumento da transferência de calor na pele humana exposta à atmosfera circundante