Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 17

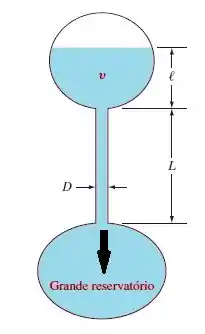
Um viscosímetro capilar mede o tempo necessário para que um volume especificado v de líquido escoe por um tubo de vidro de pequeno diâmetro, como na figura a seguir. Esse tempo de trânsito é então correlacionado à viscosidade do fluido. Para o sistema mostrado, (a) deduza uma fórmula aproximada para o tempo necessário, considerando escoamento laminar sem perdas de entrada e saída. (b) Se L = 12 cm, l = 2 cm, v = 8 cm³ e o fluido é água a 20°C, que diâmetro capilar D resultará em um tempo de trânsito de 6 segundos?

Passo 1

E aí, gente!! Tudo bem? Essa questão aqui você vai ver que é uma maravilha, afinal, se o regime é laminar, mon amour, pode confiar que vai ser super mega tranquilo de resolver a questão!!!

Vamos escrever nossa equação de energia:

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f

Passo 2

Bem, podemos fazer simplificações aqui, por exemplo, considerando que nosso ponto 1 é a base do reservatório e o ponto 2 é o topo, podemos escrever que:

Algo muito importante é o que foi dito no enunciado que é “sem perdas de cargas na entrada e saída”, em outras palavras ele tá dizendo pra gente que a pressão no ponto 1 deve ser igual a pressão no ponto 2.

Tanto no ponto 1 quanto no ponto 2 nós temos também as velocidades podem ser aproximadas a zero, e que z 1 = L + l , enquanto z 2 = 0

p 1 ρ g + V 1 2 2 g + z 1 = p 2 ρ g + V 2 2 2 g + z 2 + h f

h f = L + l

Passo 3

(a) Para um escoamento laminar como podemos escrever h f ?

h f = 128 μ Q L π ρ g d 4

Onde para um escoamento uniforme Q = v Δ t

L + l = 128 μ v L π ρ g d 4 Δ t

Δ t = 128 μ L v π ρ g d 4 L + l

Passo 4

(b) Aplicando para um Δ t = 6   s , com água tendo suas propriedades de ρ = 998   k g / m ³ e μ = 0,001   k g / ( m . s ) , a fórmula que deduzimos na letra (a) diz que:

Δ t = 6 = 128 0,001 0,12 8   x   10 - 6 π 998 9,81 d 4 0,12 + 0,02 → d = 0,0015   m

Resposta

  1. Δ t = 128 μ L v π ρ g d 4 L + l

  2. d = 0,0015   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

SAE 50W oil at 208C fl ows from one tank to anotherthrough a tube 160 cm long and 5 cm in diameter. Estimatethe fl ow rate in m3/hr if z1 5 2 m and z2 5 0.8 m.
SAE 10W30 oil at 208C fl ows from a tank into a 2-cmdiameter tube 40 cm long. The fl ow rate is 1.1 m3/hr. Isthe entrance length region a signifi cant part of this tubeflow?
Fluid flows steadily, at volume rate Q, through a large pipeand then divides into two small pipes, the larger of which has an inside diameter of 25 mm and carries three times theflow of the smaller pi
Water at 208C fl ows by gravity through a smooth pipe fromone reservoir to a lower one. The elevation difference is 60 m.The pipe is 360 m long, with a diameter of 12 cm. Calculatethe expected fl ow r
SAE 30W oil at 208C fl ows through a straight pipe 25 mlong, with diameter 4 cm. The average velocity is 2 m/s.(a) Is the fl ow laminar? Calculate (b) the pressure drop and(c) the power required. (d)