Um viscosímetro é construído de um eixo de ponta cônica que gira em um mancal cônico, como mostrado. A folga entre o eixo e o mancal é preenchida com uma amostra do óleo de teste. Obtenha uma expressão algébrica para a viscosidade μ do óleo como função da geometria do viscosímetro (H, a e θ), da velocidade de rotação ω e do torque T aplicado. Para os dados fornecidos, determine, com base na Figura A.2 no Apêndice A, o tipo de óleo para o qual o torque aplicado vale 0,325 N.m. O óleo está a 20°C. Dica: Primeiro obtenha uma expressão para a tensão de cisalhamento sobre a superfície do eixo cônico como função de z.
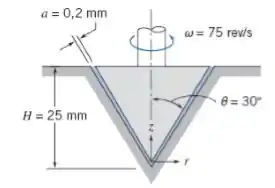
Passo 1
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Assumindo que o líquido em questão é newtoniano e que a velocidade é de perfil linear, temos que:
O torque é dado por:
Pela figura, temos que:
Logo:
Conforme subimos o dispositivo, a tensão aumenta linearmente. Sabemos que:
Logo, o torque será dado por:
Integrando de 0 até H:
Isolando-se a viscosidade e substituindo os dados: