Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 1.Problemas - Ex. 18
Para partículas pequenas a baixas velocidades, o primeiro termo na lei do arrasto de Stokes-Oseen, Problema 1.10, é dominante; portanto, , em que é uma constante. Suponha que uma partícula de massa seja obrigada a se mover horizontalmente da posição inicial com velocidade inicial . Mostre (a) que sua velocidade decrescerá exponencialmente com o tempo e (b) que ela irá parar após percorrer uma distância
Passo 1
Na letra (a), o enunciado pede para a gente mostrar que a velocidade da partícula decresce exponencialmente, então vamos precisar encontrar uma equação para a velocidade em função do tempo. Como só temos a equação da força de arraste dada pelo enunciado:
Vamos precisar mexer um pouco nela.
Como a partícula se movimento só horizontalmente, dizemos que a velocidade está no sentido de crescimento de e a aceleração produzida pela força de arraste no sentido oposto:
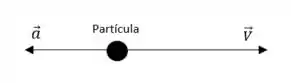
Isso significa que não precisamos usar notação vetorial, porque todo o movimento está e vai permanecer em .
Passo 2
Agora podemos usar a segunda lei de Newton para a partícula, como só a força de arraste é que está influenciando o movimento da partícula, ficamos com:
O sinal negativo aparece porque o sentido positivo está no sentido da velocidade, como a força está oposta, o sinal precisa ser negativo.
E podemos substituir ela na equação dada:
Se reescrevermos a aceleração como a derivada da velocidade em função do tempo, podemos escrever uma equação diferencial:
E se resolvermos, vamos ter:
A constante que apareceu é por causa da integração indefinida, que pode ser colocada para dentro da função logaritmo.
Aplicando a função exponencial dos dois lados:
O enunciado diz que no início do movimento, , a velocidade é , vamos substituir esses valores na equação:
Então a equação fica:
E pronto! Demonstramos que a velocidade cai com a exponencial do tempo.
Passo 3
Para a letra (b) precisamos fazer com a velocidade um processo parecido com aquele que fizemos com a aceleração na letra (a), escrevemos ela como a derivada da posição em função do tempo:
Separamos de novo:
E resolvemos as integrais:
Como pelo enunciado, a partícula sai da posição inicial , podemos achar a nova constante:
A equação fica:
Tirando fator comum:
Passo 4
Com essa equação podemos mostrar que a partícula para quando percorre a distância:
Basta fazermos tender a infinito, porque depois de determinado tempo, o arraste da força diminui a velocidade até zerar ela, e como não tem mais movimento, não tem mais arraste também e ela fica parada no ponto :