Fator de Forma
Teoria
Introdução
Quando temos duas ou mais superfícies com diferentes temperaturas e que trocam calor por radiação, calcular a taxa de calor trocada entre elas nem sempre é uma tarefa das mais fáceis.
Isso acontece porque temos que levar em consideração como esses caras estão posicionados uns em relação aos outros.
O nosso objetivo aqui vai ser justamente calcular a taxa de calor trocado entre duas ou mais superfícies.
Vamos pensar em um forno de forma cilíndrica, com . As superfícies do topo (1), da base (2) e da lateral (3) do forno são todas negras e mantidas em temperatura uniforme de e , respectivamente.
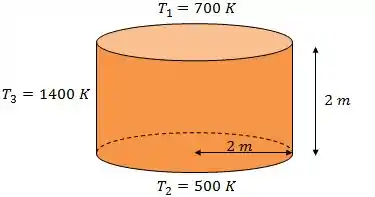
Nesse caso, qual é a taxa líquida de transferência de calor por radiação para ou a partir da superfície superior durante a operação?
Como estamos trabalhando com radiação, já bate aquela vontade absurda de usar de cara a equação:
Sério! NÃO FAÇA ISSO!
Isso porque, como eu disse lá em cima, nós precisamos levar em consideração como cada superfície está posicionada em relação às outras. Então, vamos precisar colocar aí um fator de correção para calcular a taxa de transferência.
Fator de Forma
O fator de forma é o fator de correção que vamos precisar pra calcular a troca de calor por radiação entre duas superfícies. Ele é representado da seguinte forma:
: Fração da radiação que deixa a superfície e é interceptada pela superfície .
Os valores para fator de forma podem ser obtidos através de fórmulas tabeladas para certas situações, ou através de gráficos. Vou deixar as tabelas e os gráficos no final desse capítulo, só pra deixar tudo mais organizado, beleza?
(Se quiser, dá uma olhadinha lá e volta pra continuarmos)
Olhando pro nosso problema, adicionando os termos dos fatores de forma, temos que:
Opa! Temos um gráfico que nos ajuda a calcular o fator de forma entre as duas bases do cilindro.
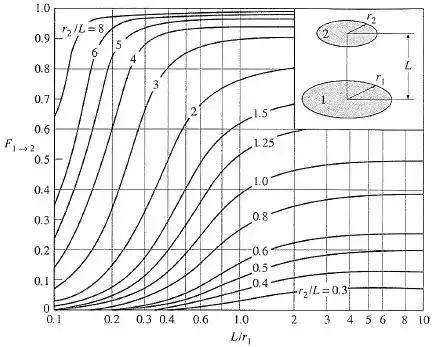
Onde:
De acordo com o gráfico:
Até aqui, tudo muito bonito! Mas não tem nenhum gráfico ou fórmula na tabela que nos ajude a calcular o fator de forma entre as superfícies 1 (topo) e 3 (face lateral)... “e agora, José?!”.
Regras do Fator de Forma
O fator de forma tem algumas regrinhas que podem salvar o dia. A primeira delas é a regra da reciprocidade, que nos diz que:
Ou seja, os fatores de forma e serão iguais somente se as suas áreas também forem iguais.
A segunda é a regra da adição, que diz que a soma dos fatores de forma de uma superfície de um recinto para todas as superfícies do recinto, incluindo a si mesmo, deve ser igual a um. Ou seja:
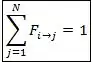
Opa! Essa nos ajuda a resolver o problema! Se liga:
Como a superfície superior é plana, , logo:
Show de bola! Resolvemos parte do nosso problema, mas vamos acabar de ver as regras do fator de forma.
A regra da superposição diz que o fator de forma de uma superfície para uma superfície é igual à soma dos fatores de forma da superfície para as partes da superfície .
A ideia é a seguinte, se eu não sei calcular o fator de forma para uma determinada superfície, mas sei calcular os fatores de forma para as partes dela, posso fazer o seguinte, então:
Pra fechar, temos a regra da simetria, que nos diz que se as superfícies 2 e 3 forem simétricas em relação à superfície 1, temos:
Voltando ao nosso problema...
Agora podemos finalmente calcular a taxa de transferência de calor por radiação da base superior do nosso cilindro, se liga:
Onde:
Logo:
O resultado negativo mostra que, na verdade, o calor está sendo transferido para a base superior do cilindro!
Promessa é dívida
Conforme prometido, seguem abaixo as tabelas e gráficos para cálculo do fator de forma. ;)
Fator de forma entre dois retângulos alinhados paralelos do mesmo tamanho:
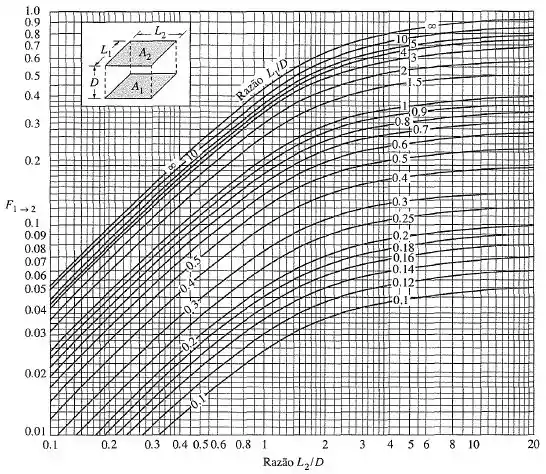
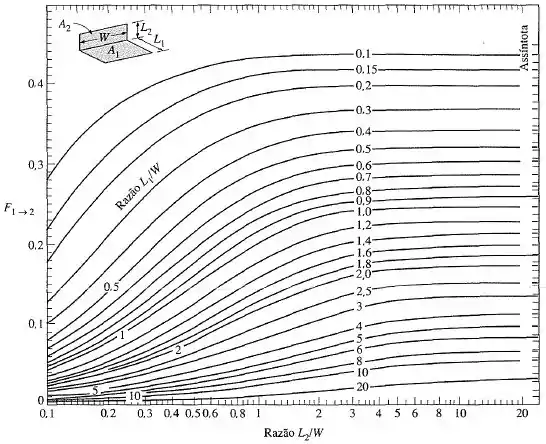
Fator de forma entre dois retângulos perpendiculares com uma aresta comum:
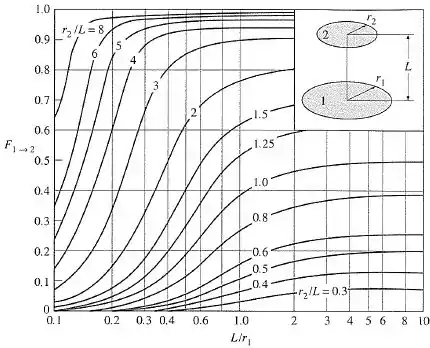
Fator de forma entre dois discos coaxiais paralelos:
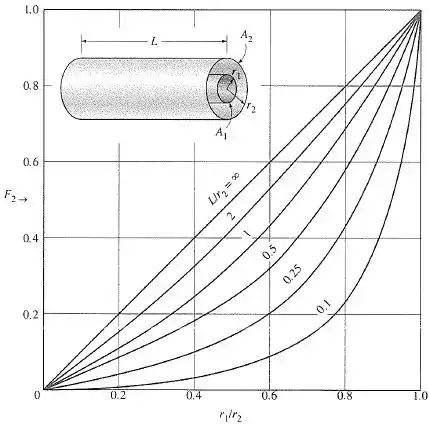
Fator de forma entre dois cilindros concêntricos de comprimento finito, do cilindro externo para o cilindro interno:
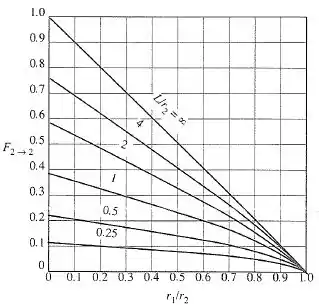
Do cilindro externo para ele mesmo:
Fator de potência para geometrias infinitamente longas (2D):
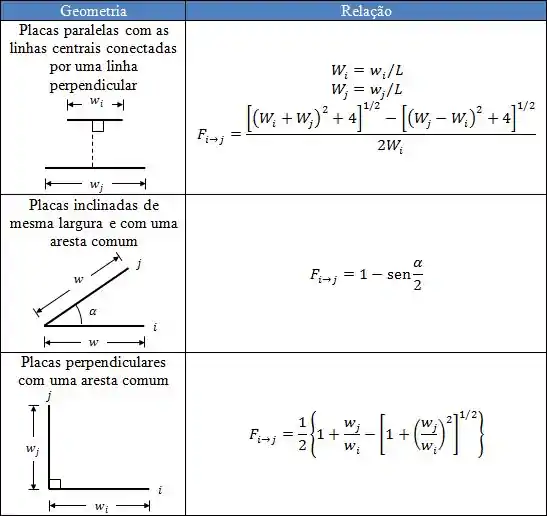
Os gráficos foram retirados do livro “Transferência de Calor e Massa – Uma Abordagem Prática” de Yunus A. Çengel.
Fator de Forma F i j
Regras do Fator de Forma
Voltando ao nosso problema...
Promessa é dívida
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Determine e para o duto longo abaixo usando a regra da reciprocidade e outras relações básicas do fator de forma.
Não utilize tabelas ou gráficos.
Passo 1
De acordo com a regra da adição:
No entanto, devido ao posicionamento das placas da superfície , nenhuma radiação emitida por incidiria sobre ela mesma, logo:
Sendo assim:
Passo 2
Para determinar o fator de forma , podemos usar a regra da reciprocidade, dada por:
Onde:
Logo:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Determine e para a pequena esfera com área sob uma hemisfera concêntrica com área , usando a regra da reciprocidade e outras relações básicas do fator de forma.
Não utilize tabelas ou gráficos.
Passo 1
Nesse tipo de casos, a melhor estratégia é “fechar” o desenho, isso costuma ajudar muito a resolver o problema.
Sendo assim, vamos inventar uma hemisfera com área para fechar a hemisfera do desenho, se liga:
Pela regra da adição, temos que:
No entanto, como se trata de uma esfera, a superfície não consegue emitir nenhuma radiação que incida sobre ela mesma, logo:
Além disso, como a hemisfera que inventamos (em pontilhado) é igual à hemisfera , podemos afirmar que:
Sendo assim:
Passo 2
Utilizando a regra da reciprocidade:
Segundo o enunciado , logo:
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
(Adaptado) Determine , , , e para a configuração hemisfera-disco abaixo usando a regra da reciprocidade e outras relações básicas do fator de forma.
Não utilize tabelas ou gráficos.
Passo 1
Como o disco e a coroa circular estão no mesmo plano, a radiação emitida por uma não irá incidir sobre a outra, ou sobre ela mesma, logo:
Sendo assim, aplicando a regra da adição a essas duas superfícies:
Passo 2
Aplicando a regra da reciprocidade para encontrar :
Passo 3
Aplicando a regra da reciprocidade para encontrar :
Passo 4
Utilizando a regra da adição para a superfície :
Substituindo os valores:
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma pista de patinação no gelo circular com de diâmetro encontra-se coberta por uma cúpula hemisférica com de diâmetro.
Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpo negro e estiverem a e , respectivamente, qual é a taxa líquida de transferência de radiação da cúpula para a pista?
Passo 1
O que queremos calcular é a taxa de transferência , dada por:
Dessa equação, nós temos tudo, exceto o fator de forma. Então vamos atrás dele!
Passo 2
A ideia aqui é a seguinte:
Por se tratar de uma pista plana, nenhuma radiação emitida pela pista é recebida por ela mesma, logo:
Assim, utilizando a regra da adição, temos que:
Utilizando a regra da reciprocidade, o fator de forma será dado por:
Como na equação da transferência de calor nós temos o produto , vou deixar esse produto desse jeito mesmo.
Mas se você preferir calcular separadamente, basta passa o termo para o outro lado, dividindo. Assim:
Passo 3
Voltando à equação da taxa de transferência de radiação, teremos:
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma peça longa em forma de é tratada termicamente pela sua suspensão no interior de um forno tubular com diâmetro de e uma temperatura de parede de . O tem os lados com de comprimento e um ângulo de .
Se a parede do forno e as superfícies da peça puderem ser aproximadas por corpos negros e a peça se encontra a uma temperatura inicial de , qual é a taxa líquida de transferência de calor por radiação por unidade de comprimento da peça?
Passo 1
Se trabalharmos com cada aba da peça e a esfera, teremos um sistema de três corpos, vamos conseguir resolver o problema, mas teremos um certo trabalho, já que a transferência de calor se dá dos dois lados de cada aba.
Uma estratégia que pode ajudar bastante nesse caso é, ao invés de separarmos a peça em pelas abas, vamos separá-la a partir de suas superfícies interna e externa, tratando cada uma como um corpo, que está à mesma temperatura.
Assim, sendo 1 a superfície interna do , 2 a superfície externa do e a superfície cilíndrica do redor, podemos escrever a taxa de transferência de calor por radiação como:
Vamos tratar dos fatores de forma, agora.
Passo 2
Olhando para a superfície externa do , qualquer radiação emitida por ela não incide sobre ela mesmo e nem sobre a superfície interna do , sendo assim:
Dessa forma, pela regra da adição, teremos:
Usando a regra da reciprocidade, teremos:
Passo 3
Analisando a superfície interna do , nenhuma radiação emitida por ele irá incidir sobre a superfície externa, logo:
O fator de forma pode ser calculado a partir da seguinte equação tabelada:
Utilizando a regra da adição, teremos:
Utilizando a regra da reciprocidade:
Passo 4
Voltando à equação da taxa de transferência de calor:
Substituindo os valores, teremos:
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere discos negros, paralelos coaxiais, separados por uma distância de . O disco inferior, com diâmetro de , é mantido a , enquanto a vizinhança está a .
Qual será a temperatura que o disco superior, com diâmetro de , irá atingir se uma potência elétrica de for suprida ao aquecedor que se encontra na sua parte posterior?
Passo 1
A potência elétrica deve ser igual à soma das transferências de calor para o disco superior. Assim:
Onde o índice 2 está relacionado ao disco inferior e o índice 3 está relacionado à vizinhança.
Dessa equação, nós temos praticamente tudo o que precisamos, exceto os fatores de forma, então vamos atrás deles.
Passo 2
Começando pelo fator de forma , temos um gráfico que pode resolver a nossa vida mas, pra isso, precisamos calcular as seguintes grandezas:
Passo 3
Pela regra da adição:
Como o disco é uma superfície plana, nenhuma radiação emitida por ele irá incidir sobre ele mesmo. Assim:
Logo:
Passo 4
Voltando à equação que encontramos no Passo 1:
Substituindo os valores:
Jogando isso tudo na calculadora, teremos:
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma cavidade cilíndrica com diâmetro e profundidade é usinada em um bloco de metal, e as condições são tais que as suas superfícies da base e lateral são mantidas a e , respectivamente.
Aproximando as superfícies por superfícies negras, determine o poder emissivo da cavidade se e .
Passo 1
A ideia é basicamente essa:
Por definição, o poder emissivo da cavidade é dado por:
Onde é dado por:
Para resolver o problema, vamos precisar dos fatores de forma.
Passo 2
Pela regra da simetria, podemos dizer que:
E através da regra da reciprocidade, podemos dizer que
Por último, pela regra da adição:
Onde , já que, como a base é plana, nenhuma radiação emitida por ela irá incidir sobre ela mesma, logo:
Juntando todas as informações, teremos que:
Assim, a equação da taxa de transferência de radiação será:
E o poder emissivo será dado por:
Como :
Passo 3
Para calcular o fator de forma , vamos usar o gráfico, onde:
Passo 4
Substituindo os valores:
Resposta
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma linha de elementos aquecedores cilíndrico, regularmente espaçados, é usada para manter uma parede de um forno, dotada de isolamento térmico, a uma temperatura de . A parede oposta encontra-se a uma temperatura uniforme de .
A parede isolada troca calor por convecção com ar a , com um coeficiente convectivo de . Considerando que as paredes e os elementos aquecedores sejam negros, estime a temperatura de operação exigida para os elementos.
Passo 1
Analisando somente o balanço de energia na parede isolada, temos que:
Onde . Onde é o fluxo térmico que sai da parede isolada para os elementos aquecedores, e é o fluxo térmico que sai da parede isolada para a parede oposta.
Dessa forma:
Precisamos dos fatores de forma pra resolver a nossa vida.
Passo 2
Pela regra da adição, temos que:
O fator de forma é dado pela seguinte equação tabelada:
Substituindo os valores:
Passo 3
Assim, a temperatura dos elementos será:
Substituindo os valores:
