Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 14

Considere duas superfícies difusas A 1 e A 2 no interior de uma cavidade esférica com raio R . Usando os métodos a seguir, deduza uma expressão para o fator de forma F 12 em termos de A 2 e R .

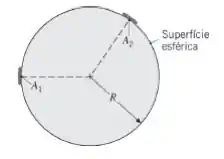
(a) Determine F 12 partindo da expressão F i j =   q i → j A i J i .  

(b) Determine F 12 usando a integral do fator de forma, Equação 13.1

Passo 1

Nessa questão nós temos suas pequenas superfícies difusas, A 1 e A 2 no interior de uma cavidade esférica com raio R .

A partir disso, vamos encontrar a expressão para o fator de forma F 12 em termos de A 2 e R por dois métodos: começando com a expressão F i j =   q i → j A i J i e usando a integral de fator de visão, Eq. 13.1

Passo 2

Para resolver essa questão vamos assumir que as superfícies A 1 e A 2 são difusas e A 1 e A 2 < <   R 2 . O fator de forma é definido como a fração de radiação que sai de A i que é interceptada pela superfície j   e pode ser expressa como:

F i j =   q i j A i J i

Da Eq. 12.11, a radiação deixada interceptada por A 1 e A 2 na superfície esférica é:

q 1 → 2 = J 1 π . A 1 cos ⁡ θ 1 .   ω 2 - 1

Onde o ângulo sólido A 2   que subtende em relação a A 1 é:

ω 2 - 1 = A 2 , n r 2 = A 2 cos ⁡ θ 2 r 2

Passo 3

Temos que,

cos ⁡ θ 1 = cos ⁡ θ 2

r = 2 R cos ⁡ θ 1

Portanto, o fator de forma é:

F i j = J 1 π A 1 cos ⁡ θ 1 . A 2 cos ⁡ θ 2 / 4 R 2 cos ⁡ θ 1 A 1 J 1 = A 2 4 π R 2

Passo 4

O fator de forma integral para as pequenas áreas A 1   e A 2 é:

F 12 = 1 A 1 ∫ A 1 ∫ A 2 cos ⁡ θ 1 . cos ⁡ θ 2 π r 2 d A 1 d A 2 = cos ⁡ θ 1 . cos ⁡ θ 2 A 2 π r 2

E,

F 12 = A 2 4 π R 2

Resposta

  1. F i j = A 2 4 π R 2
  2. F 12 = A 2 4 π R 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza expressões para o fator de forma F12 associado aos arranjos a seguir. Expresse os seus resultados em termos de A1, A2 e qualquer outra área de superfície hipotética apropriada, assim como do fa
Determine F12 e F21 para as seguintes configurações usando o teorema da reciprocidade e outras relações básicas do fator de forma. Não utilize tabelas ou gráficos.Duto longo:Pequena esfera com área A1
Dois objetos convexos estão no interior de um grande recipiente, no qual há vácuo. As paredes do recipiente são mantidas a T 3=300K . Os objetos têm a mesma área, igual a 0,2m 2 , e a mesma emissivida
Considere a cavidade composta por quatro superfícies cinzas e difusas, com todos os lados iguais, mostrada na figura. As temperaturas de três superfícies são especificadas, enquanto a quarta encontra-
Uma sala é representada pela cavidade a seguir, onde o teto (1) tem uma emissividade de 0,8 e é mantido a 40°C por elementos aquecedores elétricos nele embutidos. Também são usados aquecedores para ma