Em uma planta para a produção de enzimas por fermentação semi-sólida, a separação do material sólido (meio fermentado e micélio fúngico) do extrato enzimático líquido pode ser realizada empregando-se um filtro rotativo a vácuo com pré-capa de perlita. Em um ensaio com filtro folha de área filtrante igual a , obteve-se, após dois minutos de operação, um volume de fitrado igual . Pede-se calcular o fluxo de filtrado, a área efetiva de filtração e as dimensões do filtro Dorr-Oliver industrial, sabendo-se que se deseja obter uma vazão de extrato enzimático igual a e o filtro industrial irá operar com uma submersão de do diâmetro do tambor.
Passo 1
Vamos organizar nossas informações primeiro. Do ensaio em filtro folha, sabemos que , e obteve-se um volume de filtrado de Como vazão é volume por tempo:
Daí:
O enunciado pede fluxo de filtrado, a área efetiva de filtração e as dimensões do filtro Dorr-Oliver industrial e diz que quer . Vou passar o para as mesmas unidades:
Para dar as dimensões do filtro Dorr-Oliver, vamos precisar dessa tabelinha do fabricante:
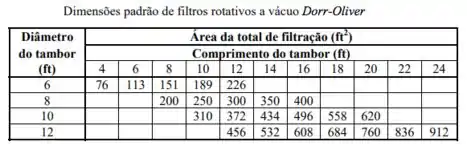
Informa também que o filtro opera com submersão de do diâmetro do tambor. Usando aquele gráfico lá da teoria:
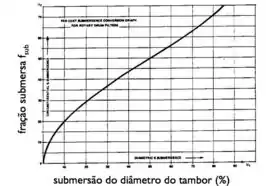
Passo 2
Para mudança de escala em filtro de tambor rotativo a vácuo, usamos:
Como o enunciado diz que o filtro tem pré capa:
O enunciado especifica , daí:
Como já vemos que na tabela do fabricante ele usa área em , vou converter logo:
Para calcular a área total de filtração, usamos o fator de submersão (em base unitária!):
Por fim, vemos a tabela do fabricante para dar as dimensões do filtro.
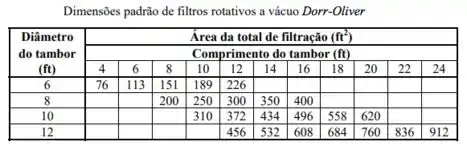
Repara que não tem o valor de , então selecionamos o filtro que oferece área filtrante imediatamente maior, que é o que oferece . Se escolhêssemos menor, teríamos uma vazão tratada menor do que a exigida. Daí: