Filtro de tambor rotativo a vácuo
Produzido por Marcelo AlvesTeoria
Introdução
Vimos na teoria anterior que filtros prensa operam em batelada. E se quisermos uma operação em contínuo? Aí temos o filtro de tambor rotativo a vácuo. Ele é um tambor oco com uma parede lateral que fica girando. Esse filtro é dividido em algumas áreas:
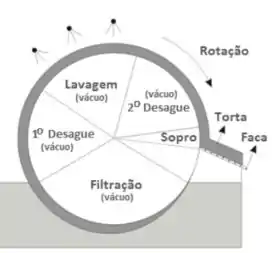
Operação
O filtro fica parcialmente submerso num tanque com a suspensão a ser filtrada, que é alimentada continuamente; faz-se vácuo dentro do tambor e o fluido entra e as partículas ficam retidas na superfície da parede lateral.
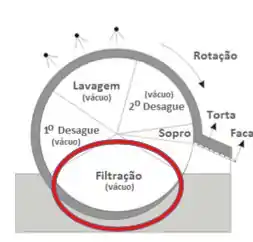
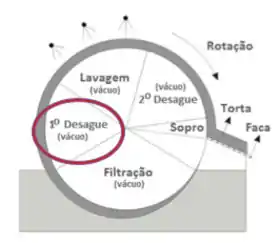
Depois dessa etapa de filtração tem desague, que é manter o vácuo mesmo sem novas partículas se aderindo na superfície, já que não mais há submersão. Faz isso pra tirar melhor o fluido dessa torta.
Às vezes, é necessária a lavagem da torta. Relembrando possíveis motivos: querer a torta mais livre do fluido da suspensão ou querer recuperar algum produto dissolvido no fluido original. Repara que mesmo durante a lavagem o vácuo continua, pra já ir secando a torta.
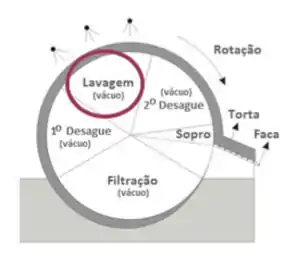
Depois de lavar vamos continuar com o vácuo por mais um pouco pra dar mais uma secadinha na torta.
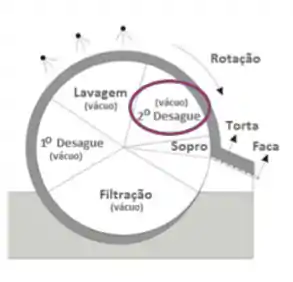
Nesse momento, a torta já está “pronta”. Precisamos soltá-la do filtro. Vai ter tipo uma placa bemmm próxima da superfície lateral do cilindro pra ir raspando a torta; essa é a faca. E, quando a torta for grudenta, tem uma região de sopro pra desgrudar um pouco a torta logo e facilitar o trabalho da faca.
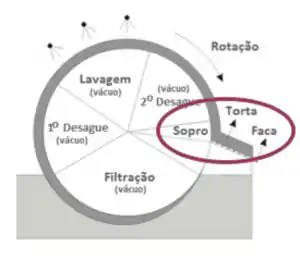
Limitações
A operação em contínuo traz uma série de benefícios, como a simplicidade e inexistência do tempo de parada (pra desmontar, limpar, remontar etc), mas há algumas limitações de uso pro filtro de tambor rotativo a vácuo; as mais importantes são:
- Queda de pressão limitada; como está trabalhando com diminuição da pressão atmosférica, pode diminuir no máximo né. Daí se tiver uma suspensão viscosa que precise de um grande, este filtro não é o indicado.
- Não indicado pra suspensões próximas ao ponto de ebulição porque aí quando fizer o vácuo, diminuir a pressão, o fluido vai entrar em ebulição
- Operação contínua NÃO é indicada se a alimentação for irregular ou o volume a ser processado for pequeno
Tempo de um ciclo
Um ciclo, isto é, um giro do tambor é composto por três partes básicas:
- Formação da torta
- Lavagem
- Secagem
O tempo total de um ciclo vai ser a soma dos tempos gastos em cada uma dessas etapas.
Se nada mais específico for mencionado, tem algumas relações que podemos usar para esses tempos:
- Em condições “normais” de operação:
- Quando se deseja uma torta seca:
- Quando a lavagem é importante:
- é a área efetiva submersa no tanque de suspensão. Lembra lá do começo que eu te disse que só uma parte do cilindro fica submersa.
- é o fator de escala, que vai, basicamente, funcionar como um fator de segurança.
Dimensionamento
Assim como em filtros prensa, vamos dimensionar baseados em experimentos; a diferença é que, aqui, vamos nos basear nos resultados obtidos em filtro folha, que é alguma coisa que você possa fazer vácuo de um lado e ter meio filtrante no outro. E aí mergulha-se o filtro folha numa suspensão e começa a fazer vácuo.
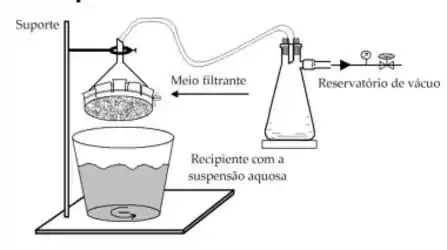
O que nos interessa nesse experimento é medir os tempos de lavagem e secagem, que serão IGUAIS no filtro de tambor rotativo a vácuo, e medir o experimental, ou seja, vazão de filtrado por área de meio filtrante. Baseado neste último, achamos o do filtro industrial por:
Calma que eu explico o que são esses termos novos aí:
Pré capa é aquela mesma ideia que vimos na teoria de filtro prensa de ter um auxiliar de filtração entre o meio filtrante a torta.
Área lateral do tambor
Com o dimensionamento, vamos achar a área submersa do tambor, mas na hora de mandar fazer o tambor vamos precisar é da área lateral dele. Achamos essa área por uma fórmulinha:
Em que é a fração submersa da área lateral do tambor. Relaxa que tem um gráfico pra acha-la, baseado na porcentagem submersa do diâmetro.
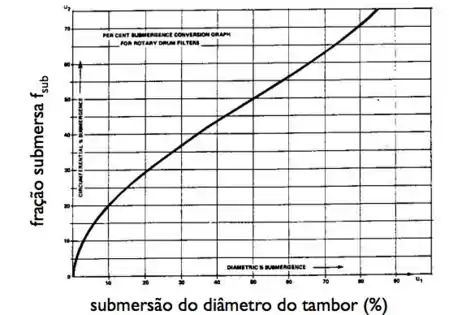
O gráfico poupa tempo, mas sinta-se à vontade pra usar geometria se preferir haha