Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Aceleração Média

Ver Todos os Exercícios

Teoria

A aceleração média é uma grandeza física que mede a variação média da velocidade de um objeto em relação ao tempo.

Fórmula da Aceleração Média

A aceleração média , como o nome já diz, é um valor médio da aceleração de um corpo durante um trajeto em determinado tempo. E matematicamente é definida como:

Onde:

  • é a aceleração média, que queremos calcular
  • é a variação de velocidade;
  • é a velocidade que o objeto em análise alcançou no final do trajeto;
  • é a velocidade que o objeto em análise iniciou o trajeto;
  • é o intervalo de tempo que o objeto demorou para percorrer o trajeto;
  • é o tempo que o objeto chegou ao final do trajeto;
  • é o tempo que o objeto iniciou o trajeto.

O Responde Aí preparou um vídeo super completo com tudo o que você precisa saber sobre Aceleração Média, pra arrasar na prova de Física! Olha só 👇👇👇

📢 Clique para saber mais:

Exemplo: Qual a aceleração média de um ciclista que ao avistar uma situação de perigo, passou da velocidade para em ?

Pra começar, vamos fazer um esqueminha do problema:

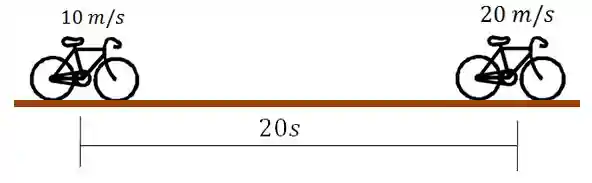
Aceleração Média: Exemplo
Aceleração Média: Exemplo

Vamos anotar o que o problema nos forneceu:

Bom, a questão nos fornece diretamente o intervalo de tempo que a bicicleta (objeto) saiu de uma velocidade para outra, então não precisamos calcular isso. Mas, ela não forneceu diretamente a variação de velocidade, na verdade ela deu a velocidade inicial e a final e, assim, conseguimos calcular a variação:

E agora podemos calcular a aceleração média pela fórmula:

O que acabamos de calcular foi a aceleração média naquele intervalo de tempo, isso quer dizer que nesse intervalo de tempo a bicicleta pode ter acelerado mais que a  nos primeiros  e menos que a  nos últimos , dando uma aceleração média de  no intervalo de , sacou?

🚨 IMPORTANTE: Podemos classificar o movimento de acordo com o valor da aceleração.

  • Se a aceleração é zero, dizemos que o movimento é uniforme porque a velocidade não varia com o tempo;
  • Se aceleração é maior que zero, dizemos que o movimento é acelerado, pois a velocidade aumenta com o tempo;
  • Se a aceleração é menor que zero, dizemos que o movimento é retardado, pois a velocidade diminui com o tempo

Aceleração Média: Análise Gráfica

É possível achar a aceleração média por um gráfico de . A aceleração será o coeficiente angular da reta nesse gráfico:

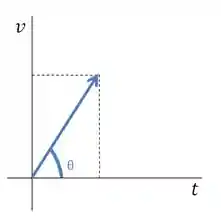
Gráfico de velocidade por tempo
Gráfico de velocidade por tempo

Matematicamente, dizemos que:

Aceleração Média x Aceleração Instantânea

Além da aceleração média podemos também calcular a aceleração instantânea.

A principal diferença entre aceleração média e instantânea esta no intervalo de tempo. A aceleração instantânea é definida para intervalos de tempo muito pequenos, próximos de zero, ou seja, ela é a aceleração média quando o tente a zero.

Vamos partir agora para os exercícios?

Aceleração Média x Aceleração Instantânea

Exercícios Resolvidos

Exercício Resolvido #1

Mundo Educação

Leia as seguintes afirmações a respeito da aceleração.

I) A aceleração é uma grandeza escalar, definida pela razão entre a variação da velocidade e variação do tempo.

II) A aceleração determina a taxa de variação das posições de um móvel.

III) A aceleração é uma grandeza vetorial, sua determinação depende da razão entre a variação da velocidade e a variação do tempo.

Está certo o que se afirma em:

a) I

b) II

c) III

d) I e II

e) II e III

Passo 1

Vamo analisar cada uma separadamente, beleza? Simbora:I) A aceleração é realmente definida pela razão entre a variação da velocidade e variação do tempo, mas ela é uma grandeza vetorial, ou seja, tem módulo, direção e sentido!

II) A nossa aceleração é dada por a = ∆ v ∆ t , então aceleração determina a taxa de variação da velocidade de um móvel.

III) Certinho e perfeitinho! SHOWWWW!

Resposta

c) III

Exercício Resolvido #2

Elaboração Própria

Qual é a aceleração de um automóvel que parte do repouso e atinge a velocidade de 108km/h em 10s?

  1. 10,8 m / s 2
  2. 3 , 0 m / s 2
  3. 4,2 m / s 2
  4. 6,0 m / s 2
  5. 5,0 m / s 2

Passo 1

Vamo nessa! A gente já sabe que:

a = ∆ v ∆ t

Show! Agora é só aplicar, certo? ERRADOOOO! Cuidado nas Unidades! Nosso tempo ta em segundos (s) e nossa velocidade em km/h, então temos que tranformar essa velocidade pra m/s. E como a gente faz isso? Dividindo por 3,6, lembra? Então vamo lá:

v = 108 3,6 = 30 m / s  

Agora podemos aplicar tudinho! Vamo lá, como nosso automóvel partiu do respouso, v i n i c i a l = 0 .

a = v f i n a l - v i n i c i a l ∆ t

a = 30 - 0 10

a = 3 m / s 2

Fechamosssss!

Resposta

b) 3,0 m / s 2

Exercício Resolvido #3

Elaboraçãp Própria

Determine o módulo da aceleração, em m / s 2 , de um móvel que gastou 2   s para aumentar sua velocidade, de   9   m / s para  21   m / s .

a) 2

b) 3

c) 4

d) 5

e) 6

Passo 1

A gente aprendeu que:

a = ∆ v ∆ t

a = v f i n a l - v i n i c i a l ∆ t

Então:

a = 21 - 9 2

a = 6 m / s 2

Shooooowwww!

Resposta

e) 6

Exercício Resolvido #4

Brasil Escola

Durante uma viagem, um caminhão possui velocidade inicial de 100 Km/h. Quando ele avista na pista uma placa indicando um radar a 1 km de distância. Nesse momento, ele pisa no freio e atinge a velocidade máxima permitida no local, que é 80 km/h no intervalo de tempo de 5s. Calcule a aceleração desse caminhão.

Passo 1

Como a gente já viu...:

a = ∆ v ∆ t

Show! Então nosso ∆ v = v f i n a l - v i n i c i a l → 80 - 100 = - 20 k m / h

MASSSS nossa velocidade precisa estar em m/s, devido ao tempo dado que foi também em segundos! Então...

v = 20 3,6 = 5,56 m / s

Agora podemos aplicar tudo certinho! Vamo lá:

a = - 5,56 5

a = - 1,1 m / s 2

Show dimaiiiI!

Resposta

a = - 1,1 m / s 2

Exercício Resolvido #5

IFSP

Um dos carros mais rápidos do mundo é o Bugatti Veyron, que alcança a velocidade máxima de aproximadamente 410 km/h, conseguindo chegar de zero a 99 km/h em aproximadamente 2,5 s. Nesse intervalo de tempo, podemos concluir que a aceleração escalar média do carro é, em m/s2, aproximadamente de:

a) 9.

b) 11.

c) 13.

d) 15.

e) 17.

Passo 1

Como a gente já decorou isso aqui de tanto usar:

a = ∆ v ∆ t

A gente esquece o nome da gente mas não esquece mais isso né? :p

Show! Então como o carro partiu do repouso, temos ∆ v = v f i n a l - v i n i c i a l → 99 - 0 = 99 k m / h

Mas nossa velocidade nesse caso precisa estar em m/s, lembra?

v = 99 3,6 = 27,5 m / s

Agora vamos jogar na fórmula!

a = 27,5 2,5

a = 1 1 m / s 2

Bom dimai Juniuuuu!

Resposta

b) 11.

Exercício Resolvido #6

Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 52 - Modificado

Um astronauta saiu da estação espacial Internacional para testar um novo veículo espacial. Seu companheiro permanece a bordo e registra as seguintes variações de velocidade, cada uma ocorrida no intervalo de 10   s . Determine a aceleração média em cada intervalo.

a) No início do intervalo o astronauta se move para direita ao longo do eixo O X com velocidade de 15   m/s e no final do movimento ele se move para direita com velocidade de 5   m/s .

b) No início do intervalo o astronauta se move a 5   m/s para esquerda e no final se move para esquerda com velocidade de 15   m/s .

c) No início do intervalo ele se move para direita com velocidade de 15   m/s e no final ele se move para esquerda com velocidade de 15   m/s .

Passo 1

Nos três itens foi pedido a aceleração média a m e para calculá-la precisamos da variação da velocidade Δ v   e a variação do tempo Δ t .

a m = Δ v Δ t

O enunciado nos informa que:

Δ t = 10   s

Então vamos usar a mesma fórmula em todos itens

a m = Δ v 10   s

Apenas mudando o valor de Δ v  

Passo 2

a Vamos encontrar Δ v   então,

Temos que

Δ v = v f - v 0

O enunciado nos informou que no inicio v 0 ele se movia a 15   m / s     e no final v f a 5   m / s     na mesma direção e sentido de v 0 .

Vamos adotar que o sentido do movimento é para direita, assim qualquer movimento para a direita será positivo e qualquer movimento para esquerda será negativo.

Agora temos tudo para calcular Δ v  

Δ v = 5 - 15

Δ v = - 10   m / s

Usando a fórmula da a m

a m =   - 10   m / s 10   s  

a m =   - 1   m / s 2

Neste caso a aceleração deu negativa porque a velocidade está diminuindo.

Passo 3

b Faremos o mesmo neste item

O enunciado nos diz que

v 0 =   - 5   m / s e v f = - 15   m / s

Ambas velocidades são negativas porque são contrarias ao sentido que adotamos.

Aplicando a equação temos:

a m = - 15 - - 5   m / s   10 s

a m =   - 1   m / s 2

Já neste caso a aceleração deu negativa pois o corpo está aumentando sua velocidade, porém no sentindo contrário ao do movimento.

Passo 4

c

O enunciado nos fornece que:

v 0 = 15 m/s e v f = - 1   5   m / s

Como v 0 está no sentindo do movimento, é positivo, mas v f   está no sentido oposto e por isso é negativo.

Pela fórmula temos

a m = - 15 - 15   m / s 10   s

a m =   - 3   m / s 2

Neste caso temos dois momentos um momento que o corpo freia (diminui a velocidade), ou seja, ele passa de 15   m / s     para 14 ,   13 … até chegar em 0 . Nesse momento a a m < 0

Onde começa o segundo momento, em que o corpo começa a aumentar sua velocidade, porém no sentido oposto ao do movimento que adotamos. Neste momento também temos a m < 0 .

Resposta

a   a m =   - 1   m / s 2

b   a m =   - 1   m / s 2    

c   a m =   - 3   m / s 2

Exercício Resolvido #7

FMTM-MG

Um cientista, estudando a aceleração média de três diferentes carros, obteve os seguintes resultados:

O carro I variou sua velocidade de v para 2v em um intervalo de tempo igual a t;

O carro II variou sua velocidade de v para 3v em um intervalo de tempo igual a 2t;

O carro III variou sua velocidade de v para 5v em um intervalo de tempo igual a 5t.

Sendo, respectivamente, a1, a2 e a3 as acelerações dos carros I, II e III, pode-se afirmar que:

  1. a 1 = a 2 = a 3
  2. a 1 > a 2 > a 3
  3. a 1 < a 2 < a 3
  4. a 1 = a 2 > a 3
  5. a 1 = a 2 < a 3

Passo 1

Bom, pra gente começar a gente pode calcular a aceleração em cada um dos casos!

No carro I:

a 1 = ∆ v ∆ t = 2 v - v t = v t

No carro II:

a 2 = ∆ v ∆ t = 3 v - v 2 t = 2 v 2 t = v t

No carro III:

a 3 = ∆ v ∆ t = 5 v - v 5 t = 4 v 5 t

Então temos

a 1 = a 2 > a 3

Resposta

d)   a 1 = a 2 > a 3

Exercício Resolvido #8

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 34-22- Modificado

De t = 0   a t = 5   m i n um homem fica em pé sem se mover; de t = 5   m i n   a t = 10   m i n ele caminha em linha reta com uma velocidade de 2,2   m / s . Quais são a sua aceleração média no intervalo de 2   m i n a 8   m i n ⁡ ? ( b ) a m é d   no intervalo de tempo de 3   m i n   a 9   m i n   ? c Plote v   em função de   t   , e indique como a resposta de ( b ) podem ser obtidas a partir do gráfico.

Passo 1

Tanto no item a quanto no b o problema pede a aceleração média a m então vamos usar a mesma equação para resolver ambos

a m = Δ v Δ t  

Passo 2

a o intervalo dado é de 2   m i n a 8   m i n , por isso temos

Δ t = 6   m i n  

Ainda pelo enunciado sabemos que a v 2 min ⁡ = 0   , pois o homem está parado, e a v 8 min ⁡ = 2,2   m / s    

Δ v = 2,2   m / s    

Precisamos passar o tempo para segundos, assim achamos

Δ t = 6.60 = 360   s

Agora podemos aplicar a equação da a m

a m = 2,2   m / s 360   s

a m = 0,0061   m / s 2    

Passo 3

b Vamos observar que o Δ t   continua o mesmo

Δ t = 9 - 3   m i n = 6   m i n  

Passando para segundos temos:

Δ t = 360   s

E o Δ v   também

Δ v = 2,2   m / s

O que implica que a a m é a mesma

a m = 0 ,   0061   m / s 2

Passo 4

Vamos fazer o gráfico de velocidade x tempo :

Sabemos que ele não se move até 5   m i n   e depois disso se move com v = 2,2   m / s , assim temos:

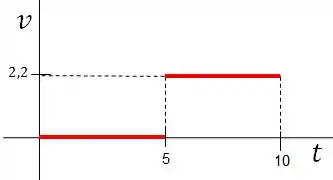
Vamos traçar uma reta entre os pontos estudados 1 º   t = 3   ,   v = 0 ; 2 º   t = 9 ,   v = 2,2   m / s

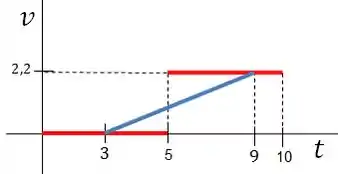
Agora Calculando a tangente da reta azul teremos a a a m

T a n θ = a m = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e

a m = 2,2   m / s 6   m i n

Já calculamos isso, e por isso quando transformarmos o tempo em segundo teremos

a m = 0,0061   m / s 2

Resposta

a   a m = 0,0061   m / s 2

b   a m = 0,0061   m / s 2

Exercícios de Livros Relacionados

Em um certo instante de tempo, uma partícula tinha uma velocidadede 18m / s no sentido positivo de x ; 2,4s depois, a velocidade era 30m / s no sentido oposto. Qual foi a aceleração média da partícula
Quando nós resolvemos problemas de queda livre perto da Terra, é importante lembrar que a resistência do ar pode ter um papel importante. Se os seus efeitos são significativos, nós podemos achar respo
Você está dirigindo um carro no limite de rapidez de 25m i / h , quando você observa um sinal na interseção a 65m de você ficar amarelo. Você sabe que, naquela interseção em particular, o sinal fica a
Uma partícula se move ao longo do eixo x com a velocidade v x = ( 8,0m / s 2 ) ⋅ t - 7,0m / s . (a) Encontre a aceleração média para dois diferentes intervalos de um segundo, um começando em t = 3,0s
Calcule a velocidade e a aceleração de um corpo situado na linha do equador, decorrentes do movimento de rotação da Terra, considerando que a circunferência desta vale 40000k m .