Velocidade Instantânea
Produzido por Ludovic BeghinTeoria
A Velocidade Instantânea é a velocidade de um objeto em um intervalo de tempo muito pequeno, tão pequeno que dizemos que ele tende a zero!
Bora entender o que isso significa?
Como Calcular a Velocidade Instantânea?
Quando começamos a estudar física e o movimento dos objetos uma das primeiras coisas que aprendemos é a velocidade média. Por definição, a velocidade média é a variação da posição sobre a variação do tempo:
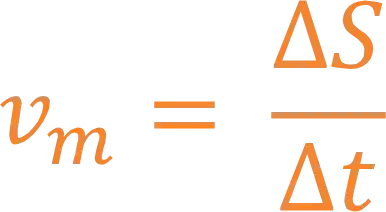
Mas como a gente faria se quiséssemos saber a velocidade de um objeto em um tempo
É ai que entra a velocidade instantânea! Pegamos a fórmula da velocidade média e tendemos o intervalo de tempo a zero, assim:
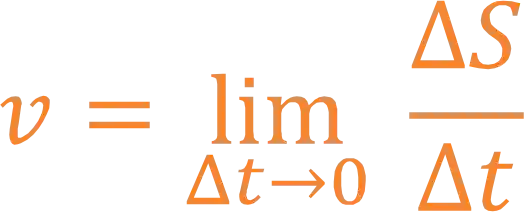
Opa, mas essa é a definição de derivada!
Fórmula da Velocidade Instantânea
A velocidade instantânea é definida como a derivada da posição em relação ao tempo:
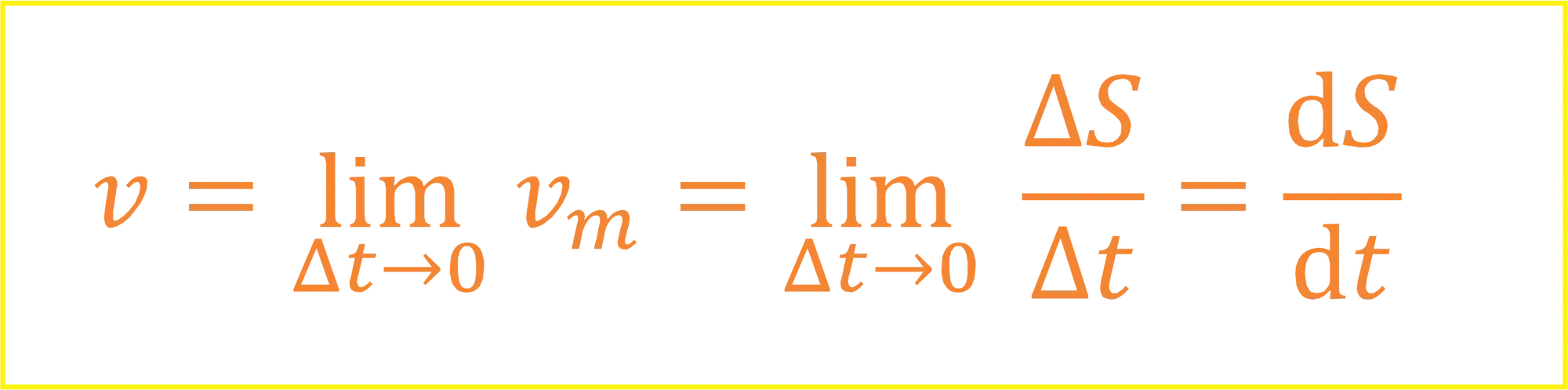
Então, se você tiver uma função posição e derivá-la em função do tempo, obterá uma função velocidade que lhe dará a velocidade instantânea!
📢Clique para ver mais:
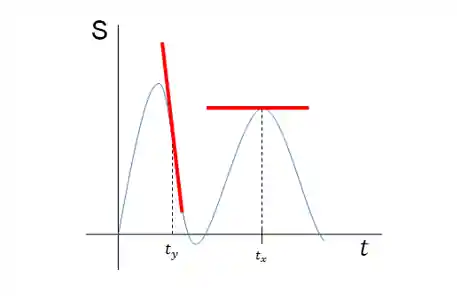
Velocidade Instantânea: Gráficos
A derivada de uma função em um ponto
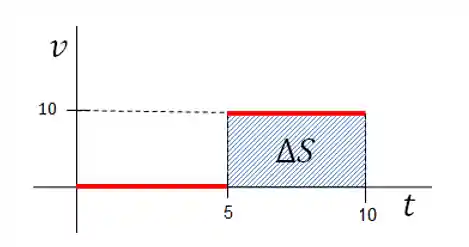
Além disso, se tivermos um gráfico da velocidade versus tempo, a área sob a curva do mesmo nos dará a variação na posição:
Aceleração Instantânea
A aceleração instantânea é o quanto a velocidade varia em um intervalo de tempo que tende a zero. Então, podemos calcula-la derivando a velocidade em relação ao tempo, assim:
Se a aceleração instantânea é a derivada da velocidade em relação ao tempo, poderíamos derivar a posição em relação ao tempo, duas vezes e chegaríamos na mesma fórmula!
Também podemos fazer o contrário. Se tivermos a aceleração, podemos integrar em relação ao tempo duas vezes, então achamos a posição!
Aceleração Instantânea: Gráficos
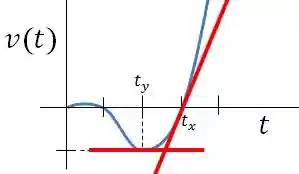
De uma forma similar ao que fizemos lá em velocidade instantânea, podemos achar a aceleração instantânea a partir da tangente do gráfico de velocidade versus tempo!
Agora vamos praticar com exercícios?!