Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 2.Exercícios e Problemas - Ex. 10
Calcule a velocidade e a aceleração de um corpo situado na linha do equador, decorrentes do movimento de rotação da Terra, considerando que a circunferência desta vale .
Passo 1
Oi pessoas, tudo certo com vocês? Espero que sim 😊. Nessa questão vamos imaginar que a partícula na linha do equador pode ser representada assim:
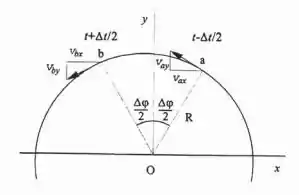
Não se assuste! É só para imaginarem que estamos trabalhando em uma circunferência, logo o raio da terra pode ser determinado por:
Passo 2
Certo, como já sabemos o raio podemos aplicar nessa equação:
Como,
Em que é o período na qual a partícula leva para completar uma volta, teremos
Substituindo na equação da velocidade, teremos:
Temos que,
Passo 3
Como já sabemos a velocidade, e sabemos que a aceleração centrípeta é dada por:
Teremos,
Resposta
;
Exercícios de Livros Relacionados
Em uma demonstração em aula, um deslizador se move ao longo de um trilho inclinado, com aceleração constante. Ele é projetado da parte mais baixa do trilho, com uma velocidade inicial. Após 8,00 s, el
A Torre da Estratosfera, em Las Vegas, tem a altura de 1137 ft. Um elevador rápido leva 1 min e 20 s para subir do térreo ao topo do prédio. O elevador inicia e termina em repouso. Suponha que ele man
Um carro de corridas pode ser acelerado de 0 a 100km/h em 4s. Compare a aceleração média com a aceleração da gravidade. Se a aceleração é constante, que distância o carro percorre até atingir 100km/h?
Um avião a jato de grande porte precisa atingir a velocidade de 500km/h para decolar, e tem uma aceleração de 4 m / s 2 . Quanto tempo ele leva para decolar e que distância percorre na pista até a dec
Um jato comercial deve atingir uma velocidade de 360k m / h para decolar. Qual é o menor aceleração constante necessária para que o avião decole de uma pista com 1,80k m de extensão?