Campo Elétrico Gerado por uma Carga Pontual
Produzido por Bruno SoaresTeoria
Introdução
Vamos ver aqui o que geram as forças descritas pela Lei de Coulomb: os chamados campos elétricos.
A carga positiva pode ser entendida como um chafariz que expele água e a carga negativa como um ralo por onde a água escoa. De forma análoga, as linhas de campo elétrico saem das cargas positivas e entram nas cargas negativas.
Calma, logo você vai entender melhor!
Vamos começar olhando para a Lei de Coulomb
Se liga nesse exemplo!
Se tivermos duas cargas, e , separadas por uma distância , então podemos calcular a força de atração ou de repulsão por meio da lei de Coulomb:
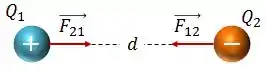
onde representa a força que faz sobre , e representa a força que faz sobre , beleza?
Para começar, vamos observar apenas a carga , reescrevendo a lei de Coulomb de forma a isolar a carga desse corpo:
Na equação acima, denominamos o módulo do campo elétrico que a carga gera no ponto em que está a carga . Note que depende apenas da carga e da distância entre as cargas.
Como eu te falei, o campo elétrico é uma grandeza vetorial. Assim, temos que encontrar a direção e o sentido do vetor campo elétrico .
Como a força e o campo são grandezas vetoriais, temos:
Note que a carga é positiva. Assim, o sentido e a direção do campo elétrico são idênticos aos da força que a carga exerce na carga .
No caso da carga negativa, ocorre o oposto:
Como a carga é negativa, a direção do campo elétrico é igual à direção da força que a carga exerce na carga , mas os sentidos são opostos.
Temos, então, a seguinte situação:
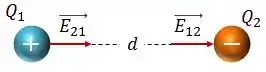
Podemos então notar que:
- O campo gerado pela carga positiva (carga ) aponta para fora dela.
- O campo gerado pela carga negativa (carga ) aponta para dentro dela.
Um detalhe importante:
Como , fica fácil determinar as unidades do campo elétrico no S.I:
Como a força é expressa em Newton , a carga é expressa em Coulombs , temos que o campo elétrico é expresso em “Newton por Coulombs” .
Campo Elétrico Gerado por uma Carga Positiva
Temos aqui uma carga elétrica puntiforme positiva (e solitária):
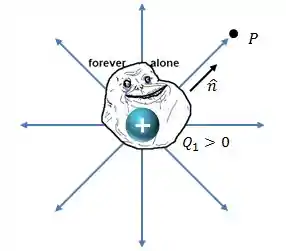
O campo elétrico gerado por num ponto situado nos arredores dessa carga é dado por:
Onde é a distância da carga até o ponto .
Observe que o vetor unitário radial aponta “para fora” da carga .
Logo, as linhas de campo elétrico “saem” da carga , apontando para fora, como indicado pelas setas azuis.
Campo Elétrico Gerado por uma Carga Negativa
Vamos agora dar uma olhada na carga solitária negativa:
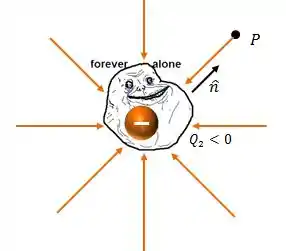
O caso é parecido e aqui o campo elétrico gerado por e que atua num ponto será dado por:
Porém, como agora a carga é negativa, então o sentido do vetor se inverte em relação ao caso da carga positiva: as linhas de campo elétrico “entram” na carga , como indicado pelas setas laranjas.
Resumindo...
Temos, então, uma diferença básica entre campos gerados por cargas positivas e os gerados por cargas negativas:
- Cargas positivas “cospem” o campo elétrico.
- Cargas negativas “sugam” o campo elétrico.
As cargas positivas podem ser comparadas a um chafariz, que solta água em todos os seus arredores.
As cargas negativas se comportam como um ralo, que suga a água dos seus arredores.
Superposição de campos elétricos
Lá na Lei de Coulomb aplicamos o princípio da superposição para casos onde tínhamos mais de duas cargas interagindo.
Esse mesmo princípio também pode ser aplicado a campos elétricos.
Vamos analisar a seguinte situação: temos uma carga positiva e outra negativa interagindo no vácuo. A boa de hoje é calcular o campo elétrico resultante dessa configuração no ponto , de acordo com a figura abaixo.
![]()
Olá!
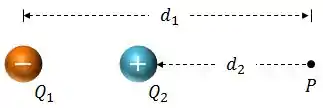
Vamos iniciar dando nomes aos bois nesse nosso exemplo:
Vamos, agora, calcular o vetor campo elétrico gerado por cada uma dessas cargas no ponto , ok?
Para as duas cargas, o vetor unitário que tomamos é o mesmo: um vetor de módulo , que aponta para a direita, como mostra a figura abaixo. Saca só!
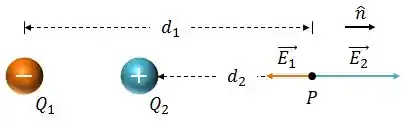
Sendo assim, o campo elétrico resultante será a soma vetorial de todos os campos elétricos, logo:
Show! Para fechar: e se colocássemos uma carga exatamente no ponto , qual seria, nesse caso, a força resultante que age sobre ela?
Bom, poderíamos fazer isso calculando a força que cada carga exerceria sobre a nossa carga e depois calcular a força resultante, ou podemos simplesmente utilizar o valor do campo elétrico resultante no ponto , que nós acabamos de calcular.
Dessa forma, a força resultante sobre a carga seria:
Entendeu numa boa? #PartiuExercitar