Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 58

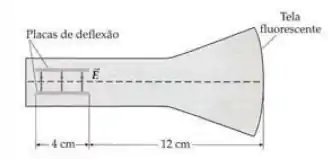
Um elétron que tem uma energia cinética igual a 2,00 × 10 - 16   J está se movendo para a direita ao longo do eixo de um tubo de raios catódicos, como mostra a Figura 21-40. Um campo elétrico E → = 2,00 × 10 4   N / C   j ^ existe na região entre as placas de deflexão e, fora desta região, o campo elétrico é nulo ( E → = 0 ). (a) A que distância está o elétron do eixo do tubo quando ele sai da região entre as placas? (b) Em que ângulo o elétron está se movendo com relação ao eixo depois da sair da região entre as placas? (c) A que distância do eixo o elétron colidirá com a tela fluorescente?

Passo 1

  1. No eixo x teremos um movimento uniforme. Já no eixo y , teremos um movimento com aceleração constante.

    2. Tal aceleração poderá ser obtida da seguinte maneira:

    F → = e E → m a → = e E → a = E q m

    Passo 2

    Dessa maneira, temos que:

  • No eixo x :

    • Δ x = v 0 t

  • No eixo y : podemos aplicar Δ y = v 0 y t + 1 2 a t 2 . Nesse caso, v 0 y = 0 . Assim:

Δ y = 1 2 a t 2

Isolando o tempo na primeira equação, temos t = Δ x / v 0 e colocando na segunda:

Δ y = E q Δ x 2 2 m v 0 2

Como K = 1 2 m v 0 2 ⟹ m v 0 2 = 2 K . Finalmente,

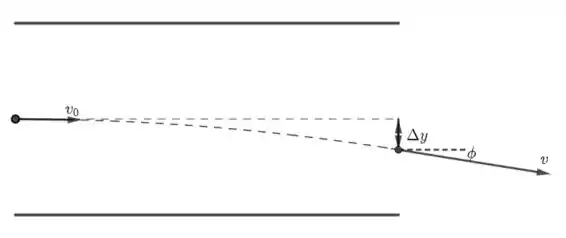
Δ y = E q Δ x 2 4 K = 2,00 × 10 4 1,6 × 10 - 19 4 × 10 - 2 2 4 2,00 × 10 - 16 Δ y = 6,40   m m

Note que esse deslocamento ocorre para baixo, como mostra a figura abaixo.

Passo 2

  • Temos

    • v y 2 = v 0 y 2 + 2 a Δ y v y = 0 2 + 2 E q m Δ y v y = 2 E q m Δ y

    Da figura, vemos

    tan ⁡ ϕ = v y v 0

    onde K = 1 2 m v 0 2 ⟹ v 0 = 2 K / m . Portanto,

    tan ⁡ ϕ = 2 E q m Δ y 2 K m = E q Δ y K tan ⁡ ϕ = 2 × 10 4 1,6 × 10 - 19 ( 6,40 × 10 - 3 ) 2,00 × 10 - 16 = 0,32

    Assim,

    ϕ = 17,7 °

    Passo 3

  • Temos que:

    • Δ y ' = Δ x ' tan ⁡ ϕ = 120   m m tan ⁡ 17,7 ° = 38,4   m m

    Dessa maneira, a altura H é dada por:

    H = Δ y + Δ y ' = 6,40 + 38,4 = 44,8   m m

    Resposta

    1. 6,40   m m
    2. 17,7 °
    3. 44,8   m m
    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Qual é o módulo de uma carga pontual cujo campo elétrico a 50 cm de distância tem um módulo de 2,0 N/C?
    Qual é o módulo de uma carga pontual capaz de criar um campo elétrico de 1,00 N/C em um ponto a 1,00 m de distância?
    Duas partículas são mantidas fixas sobre o eixo x : a partícula 1, de carga q 1 = 2,1 · 10 - 8C , no ponto x = 20c m , e a partícula 2, de carga q 2 = - 4,00 q 1 , no ponto x = 70c m . Em que ponto do
    Duas cargas puntiformes de módulos e sinais desconhecidos estão separadas por uma distância d. O campo elétrico é nulo num ponto do segmento que une as cargas. O que se pode concluir sobre essas carga
    Que dificuldades matemáticas seriam encontradas no cálculo do campo elétrico de um anel carregado em pontos que não estivesse sobre o eixo?