Campo Elétrico Uniforme
Teoria
Fala aí! Tudo tranquilo? Hoje nós vamos falar sobre campo elétrico uniforme. Sem muito segredo: um campo elétrico uniforme é aquele que tem direção, sentido e intensidade que não variam com a distância.
Não tem muita novidade aqui em relação a campo elétrico em geral, então se você caiu aqui de paraquedas 🪂 ou só tá precisando dar uma recapitulada nessa parte, dá só uma olhada no nosso conteúdo sobre campo elétrico gerado por uma carga pontual e depois volta aqui pra darmos sequência, beleza?
Não deixa de conferir também 👇😉:
Fórmula do Campo Elétrico Uniforme
Aqui não tem nenhum conceito novo muito complicado ou outra fórmula maluca pra você decorar, a única “fórmula do campo elétrico uniforme” que vamos usar aqui é aquela mesma fórmula que usamos para qualquer outro campo elétrico comum:
Com:
E
K
|Q|
d
O que é um Campo Elétrico Uniforme?
Um corpo de carga positiva gera um campo divergente, certo? Então, vamos desenhar linhas de força se afastando da placa. Dá só uma olhada:
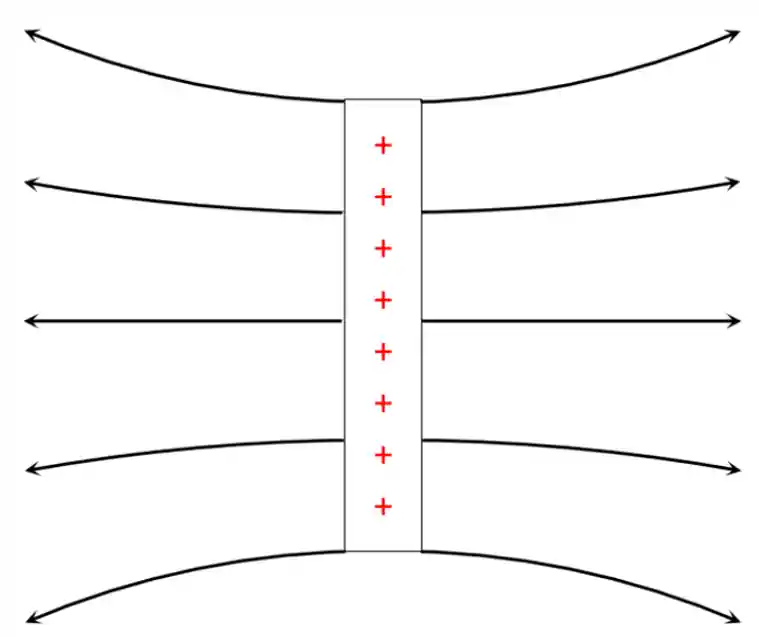
Beleza, essas setinhas que desenhei ali são as famosas linhas de força, que indicam a direção e o sentido do campo elétrico gerado pela barrinha. Reparou como elas se tornam mais afastadas umas das outras conforme se distanciam da barra? Isso ocorre porque o campo elétrico fica mais fraco nessas distâncias maiores. Quer dizer que, neste caso, o tal do campo elétrico depende, sim, da distância.
Agora, vamos pegar essa mesma figura aí em cima e focar só nesse pedacinho aqui:
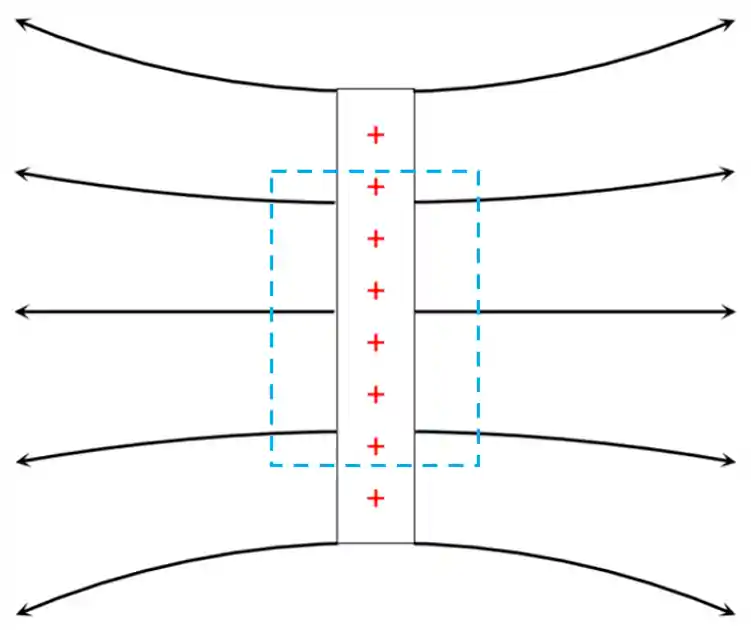
Percebe como as linhas parecem ser paralelas? Por conta disso, podemos considerar a ideia de que o campo elétrico tem o mesmo valor em qualquer ponto do espaço dentro dessa região. Isso é um exemplo de campo elétrico uniforme, percebeu como ele é constante em módulo, direção e sentido?
Campo Elétrico Entre Placas Paralelas
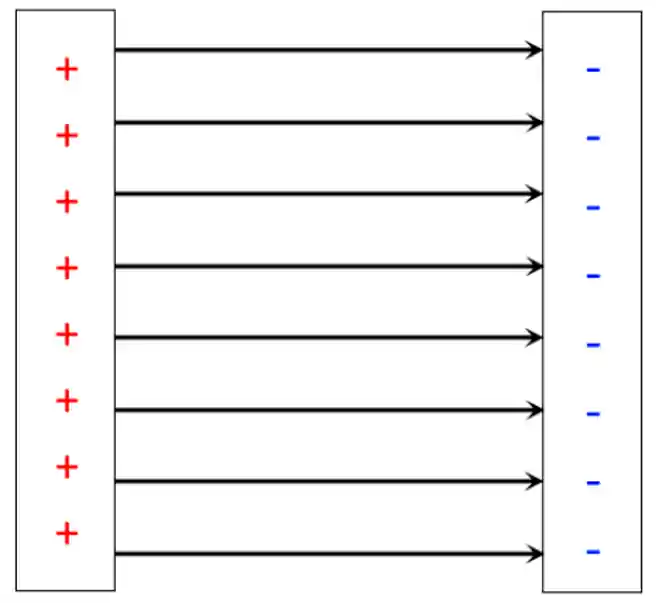
Beleza, mas quando é que isso vai ser relevante pra mim? Olha só, vamos imaginar duas placas eletrizadas posicionadas uma ao lado da outra. Mais ou menos assim:
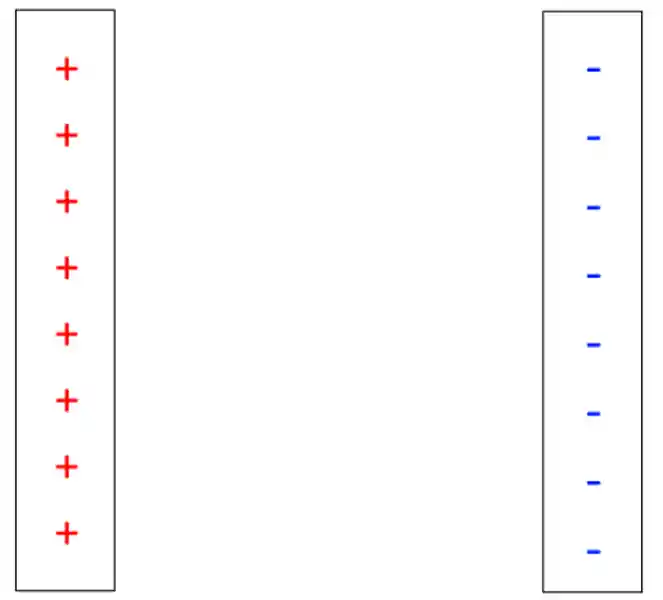
Consegue imaginar como vai ficar o campo elétrico do lado de cada placa? Pra visualizar melhor, vamos desenhar o campo de aproximação (as setinhas azuis, apontando para dentro da barra negativa) gerado pela placa carregada negativamente e o de afastamento (as setinhas vermelhas) gerado pela placa positiva. Se liga:
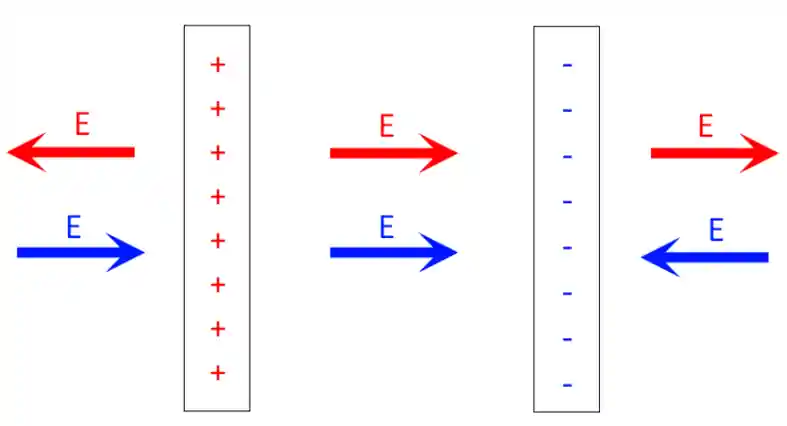
Agora, vamos considerar estas placas posicionadas bem próximas uma da outra (dentro daquela região que vimos logo acima). Com isso, podemos dizer que, naquelas regiões em que temos setinhas apontando para lados opostos, uma irá anular a outra e o campo resultante será nulo.
E na região ali entre as duas placas? O campo elétrico resultante ali nessa região aponta no sentido da placa positiva para a negativa, já que as duas setinhas estão apontando para o mesmo lado, sacou?
E aí é só desenharmos linhas de força saindo da placa positiva e entrando na negativa:
Exercícios de Campo Elétrico Uniforme
A grande maioria de questões desse tópico vai pedir pra você analisar o movimento de partículas dentro desse campo elétrico uniforme. Se liga só nesse exemplo:
Uma partícula de massa m e carga positiva q está inicialmente a uma velocidade igual a
E ainda nos foi informado que a carga faz a seguinte trajetória:
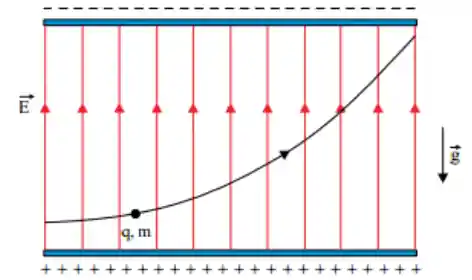
Beleza, é sempre bom começarmos esse tipo de exercício desenhando um diagrama de corpo livre. Pra essa carga aí, vamos desenhar a velocidade inicial apontando para a direita, o peso apontando para baixo e a força elétrica apontando para cima, na mesma direção do campo elétrico.
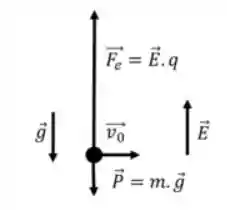
Com isso, podemos usar a Segunda Lei de Newton para escrever a força resultante para a carga:
Então, a carga acelera para cima com aceleração igual a:
No eixo
Portanto, as equações de movimento para este exemplo são:
Com essas equações, podemos resolver diversos problemas relacionados a esse caso. Por exemplo, questões que peçam para você calcular a distância que uma partícula percorre até se chocar com uma das placas, ou quanto tempo leva para que isso aconteça.
Tranquilinho? Então bora praticar mais exercícios e ficar craques no assunto 🥳
O que é um Campo Elétrico Uniforme?
Campo Elétrico Entre Placas Paralelas
Exercícios de Campo Elétrico Uniforme
Exercícios Resolvidos
Exercício Resolvido #1
UFF-Física II-Lista de Exercícios 1-Exercício n°7
O campo elétrico em certo ponto do espaço é .
Qual é a força elétrica sobre um próton posicionado neste ponto?
Qual é a força elétrica sobre um elétron posicionado neste ponto?
Qual é o vetor da aceleração do próton?
Qual é o vetor da aceleração do elétron?
Dados: ; ; e .
Passo 1
Para determinar a força exercida em um próton nesse ponto, precisamos lembrar da definição de campo:
O valor da carga do próton é . Agora ficou fácil!
Passo 2
Para o elétron, faremos a mesma coisa, só que dessa vez, temos . A força fica:
Passo 3
Agora que temos a força que é exercida no próton, achar o vetor aceleração é fácil, temos que lembrar lá de mecânica:
Temos que a massa do próton é dada por .
Agora é só substituir:
Passo 4
Para determinar o vetor aceleração do elétron, vamos usar o mesmo método que usamos no item anterior, se liga!
Sendo que a massa do elétron é , agora é só substituir!
Resposta
Exercício Resolvido #2
UFRJ-P1-2014.2-Múltipla Escolha n°3.
A figura mostra duas partículas pontuais, de cargas e e massas desprezíveis, colocados sobre os braços (também de massas desprezíveis) de mesmo comprimento de uma balança nas distâncias indicadas.
A balança está em uma região onde existe um campo elétrico uniforme vertical para baixo, conforme mostra a figura. Para que a balança permaneça em equilíbrio o valor de deve ser igual a
Passo 1
Para que a balança permaneça em equilíbrio, é necessário que o somatório dos torques em torno da articulação seja nulo. Logo:
Essas forças serão exatamente a força elétrica do campo elétrico sobre as cargas, onde:
Sendo assim:
Finalmente:
Logo, a resposta certa é a letra .
Resposta
Exercício Resolvido #3
UFF- Física II-Lista de Exercícios 1-Exercício n°15- Modificado.
Um elétron com velocidade é lançado paralelamente a um campo elétrico uniforme que o freia.
Qual a distância que o elétron percorre até parar?
Quanto tempo ele leva para parar?
Se o campo elétrico se estende por uma região de de comprimento, que fração de energia cinética inicial o elétron perde ao atravessar o campo?
Dados:
Passo 1
Para resolver essa questão, precisamos saber a força que é exercida nessa elétron quando ele passa pelo campo elétrico, para isso, vamos utilizar a definição de campo elétrico em módulo:
Sendo a carga do elétron , o módulo da força, será:
Agora que temos a força, podemos achar a aceleração que freia o elétron, sendo a massa do elétron :
Agora é só usar as equações da cinemática, simbora!
Passo 2
Para determinar quanto o elétron percorre até parar, iremos utilizar a equação de Torricelli:
Substituindo os valores, temos:
A aceleração é negativa pois ela está freando o elétron!
Passo 3
Para determinar o tempo necessário, basta utilizarmos:
Substituindo, temos:
Passo 4
Para determinar quanto da energia cinética inicial foi perdida, podemos calcular a variação de energia cinética e dividir pela energia cinética inicial, se liga!
Já que a velocidade final é menor que a inicial
Como nós já temos a velocidade a entrar no campo, , basta determinar , para isso, vamos mais uma vez utilizar a equação de Torricelli!
Só presta atenção que agora o elétron percorre uma distância (lá do enunciado!)
Como queremos , basta multiplicar por
Agora é só substituir!
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física III – Eletromagnetismo, 12ª ed. São Paulo, 2010, pp. 33- Modificado.
Um elétron é projetado com velocidade inicial para dentro do campo elétrico uniforme entre as placas paralelas indicadas na figura abaixo. Suponha que o campo seja uniforme e orientado verticalmente para baixo e considere igual a zero o campo elétrico fora das placas e despreze a força peso. O elétron entra no campo em um ponto intermediário entre as placas.
- Sabendo que o elétron tangencia a placa superior quando ele sai do campo, calcule o módulo do campo elétrico;
Dados:
Passo 1
O começo da questão é um problema de cinemática. O elétron tangenciar a placa ao sair do campo implica que o deslocamento em é igual à:
Ao passo que o deslocamento em é:
Para a componente temos um movimento de velocidade constante:
Tendo a velocidade e o deslocamento, isolamos o tempo e substituímos os valores:
Passo 2
Nesse mesmo intervalo de tempo o elétron viajou verticalmente, só que num movimento acelerado proveniente do campo elétrico. Vamos desprezar efeitos da gravidade pois a massa do elétron é muito pequena, já é?
Para a componente :
Temos o deslocamento e o intervalo de tempo.
Como inicialmente o elétron se desloca na direção horizontal a sua velocidade vertical inicial é nula
Daí segue que:
Show. Podemos inferir o valor do campo à partir da aceleração!
Passo 3
Como temos que:
E temos a aceleração e a massa (a massa do elétron é tabelada)! Podemos então descobrir o valor do campo, por conta da fórmula:
Partiu então. Como só queremos o módulo (direção e sentido já foram dadas no enunciado) vamos trabalhar só com ele mesmo:
Substituindo os valores (lembrando que a carga do elétron é tabelada também):
Finalmente!
Resposta
Exercício Resolvido #5
UNICAMP-P1-Física III-Diurno-2011-2-n°1
Duas pequenas esferas carregadas, cada uma de massa , estão suspensas por fios de comprimento , conforme diagrama abaixo. Um campo elétrico uniforme e aplicado ao longo da direção . As esferas possuem cargas iguais a e .
Determine:
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
O campo elétrico nas mesmas condições dadas no item ;
A tensão no fio nas mesmas condições dadas no item ;
Passo 1
A força elétrica em função de e , sobre cada esfera de modo que o conjunto fique em equilíbrio;
Antes de começar, vamos entender mais ou menos o que acontece nesse problema.
Temos duas esferas de cargas e que irão gerar uma força elétrica de atração entre si, vamos chamar essa força de .
Além disso, essas cargas estão sobre a presença de um campo elétrico que também irá gerar uma força elétrica nas cargas, vamos chamar essa força de .
Ambas as forças são forças elétricas e, por conta disso, vamos soma-las e chama-la de .
Agora, para encontrar o valor da força elétrica que mantêm as cargas em equilíbrio, precisamos fazer o diagrama do corpo livre:
Como o sistema está em equilíbrio, podemos dizer que:
A partir da segunda equação, podemos escrever:
Substituindo isso na primeira equação, teremos:
Passo 2
O campo elétrico nas mesmas condições dadas no item ;
Como vimos no Passo 1, a força elétrica será pela interação entre as cargas e pela interação com o campo elétrico :
A gente sabe que a força gerada por um campo uniforme tem módulo dada por:
A força de interação tem módulo
Onde é a distância entre as bolinhas.
De acordo com a geometria do problema, podemos dizer que:
Logo,
Passo 3
Agora precisamos definir o sentido dessas forças. Para isso a gente tem que lembrar que como as cargas das bolinhas são contrárias, a força de interação tende a atraí-las. Para a força do campo a gente tem que lembrar que se a carga for positiva a força tem o mesmo sentido do campo, caso contrário será o sentido oposto ao campo.
Então no nosso problema vamos ter isso aqui:
Ou seja, independente da bolinha que a gente considere, uma força é oposta a outra! Vou considerar o sentido positivo para a direita e analisar a bolinha positiva. Teremos então:
Finalmente:
Agora precisamos somente substituir a expressão da força elétrica que calculamos no item :
Passo 4
Pra terminar com isso, só falta isolar o e arrumar a bagunça:
Finalmente:
Passo 5
A tensão no fio nas mesmas condições dadas no item .
Podemos escrever a seguinte expressão para a tensão, obtida anteriormente:
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 21.84, pp. 37.
Duas minúsculas bolas de massa possuem carga de módulo , porém de sinais contrários. Elas estão atadas ao mesmo gancho de teto por fios leves, de comprimento . Quando um campo elétrico uniforme horizontal é ativado, as bolas ficam suspensas a um ângulo entre os fios, como mostra a Figura abaixo. Considere que o campo elétrico seja intenso suficiente para que a força eletrostática entre as cargas e possa ser desconsiderada.
- Qual bola (a da esquerda ou a da direita) é positiva e qual é negativa?
- Ache o ângulo entre os fios em termos de , , e ;
- À medida que a intensidade do campo elétrico aumenta, o que o resultado do item b) fornece para o maior ângulo possível?
Passo 1
a) Aqui é importante que a gente se lembre de que o campo elétrico sempre aponta das cargas positivas para as cargas negativas, como mostra a Figura abaixo. Portanto, a carga positiva se aproxima da região onde se encontra a região negativa do e a carga negativa da região positiva desse mesmo campo. Tranquilo?
Passo 2
b) Dada essa situação, na Figura acima, mostro para você como ficam os vetores das forças que atuam sobre as cargas e . Na direita da figura, a gente tem a carga isolada com as forças que atuam sobre ela representadas.
Como esta carga está em equilíbrio, a soma das forças na direção e devem ser iguais, o que dá para gente o seguinte sistema de equações:
Agora, como o enunciado diz que o campo é intenso o suficiente para que a gente despreze a força de Coulomb entre as cargas puntiformes e comparado com a força que atua nelas, podemos reescrever as componentes das forças em e como
Se a gente divide a primeira equação acima pela segunda expressão, chegamos a
Passo 3
c) Agora, a partir da expressão acima para o ângulo em função do módulo do campo , repara que a gente tem os seguintes comportamentos:
- ,
já que, quando . Isso significa que, quanto mais intenso o campo elétrico, mais o ângulo entre os dois fios se aproxima de e, com esse ângulo, os fios vão estar alinhados e as cargas estarão encostadas no teto e separadas por uma distância .
Resposta
- Carga da esquerda é positiva e a da direita negativa;
- À medida que aumenta, aumenta e, para , .
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 21.40, pp. 33.
Uma carga puntiforme está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme por meio de uma haste leve, rígida e não condutora, de comprimento . Um campo elétrico uniforme de módulo está direcionado paralelamente ao fio, como indica a Figura abaixo.
- Determine a tensão no fio?
- Qual seria a tensão se ambas as cargas fossem negativas?
Passo 1
a) Vamos lá?? A primeira coisa em que a gente precisa ficar ligado é que o campo elétrico sempre aponta das cargas positivas para as cargas negativas, como coloco na Figura abaixo para você, blz?? Por isso, a força atuando em aponta da direita para a esquerda.
A gente não precisa de preocupar com a carga positiva , porque o enunciado disse que ela está fixa a uma distância da carga . Tranquilo? Então vamos analisar com fica a tração que age em puxando-a para a direita, como tá esquematizado na Figura.
Como está em repouso, significa que temos o seguinte:
Agora, é a força de Coulomb entre as cargas separadas por . Colocando os valores fornecidos no enunciado, obtemos que:
Já para , temos que
Jogando na expressão para :
Passo 2
b) Nessa nova situação, ambas as cargas são negativas, mas com o mesmo módulo de antes. Nesse caso, como mostramos na nova Figura abaixo, a força muda de sentido, apontando, agora, da direita para a esquerda.
Aqui, a nova condição de equilíbrio das forças fica escrita como
O módulo da força entre as cargas permanece o mesmo, assim como o módulo da força !! O que muda aqui é que esse módulos são somados. Por isso, temos uma tensão mais intensa e dada por
Resposta
Exercício Resolvido #8
Elaboração própria
Uma carga positiva , com velocidade , entra na região entre duas placas paralelas numa direção perpendicular a um campo elétrico uniforme . As placas são separadas por um distância e submetidas a uma diferença de potencial , como indicado na Figura abaixo. A carga percorre todo o espaço entre as placas e sai dessa região com uma velocidade , inclinada em relação ao eixo e a uma distância desse eixo. Desprezando a força gravitacional, qual o valor da posição ? Expresse seu resultado em termos de , , , e .
Passo 1
Aqui temos uma carga positiva que entra numa região onde há um campo elétrico uniforme e apontando na direção de . Nesse caso, a carga positiva vai sentir uma força de atração em direção às placas negativas e essa força vai ter a mesma direção, sentido e módulo ao longo de todo o seu percurso no interior das placas. Blz quanto a isso?
Bom, como estamos desconsiderando a força gravitacional sobre a carga, então, da segunda lei de Newton, a gente tem o seguinte valor para a aceleração na direção :
Por outro lado, se a gente olha agora para a direção do eixo , a carga não tem aceleração, ou seja, a carga positiva tem um movimento com velocidade uniforme na direção . Isso significa que ao longo do eixo , a velocidade da partícula será sempre . Sacou?
Agora, olha só, a gente tem a mesma situação que lá no caso do movimento oblíquo de uma partícula lançada na presença de um campo gravitacional. Por isso, aqui no caso da Figura acima, a partícula carga também vai descrever uma trajetória parabólica na região dentro das placas!! IMPORTANTÍSSIMO ISSO…GUARDA AÍ COM CARINHO NO CORAÇÃO…
Tamo junto até aqui?? Segue firme comigo…
Passo 2
Como o movimento é uniformemente acelerado na direção , a equação horária para posição é
sendo que é a velocidade inicial da carga na direção . Lembrou disso?
Bom, o que a gente quer é encontrar , correto? Mas, da Figura, vemos que a posição e velocidade inicial, ambas em , são:
Substituindo isso e lembrando da expressão para a aceleração, que é , obtemos que
Tranquilo? Precisamos, agora, só colocar essa expressão em termos das quantidades pedidas pelo exercício. Vamos lá?
Passo 3
Como o movimento da carga na direção é uniforme, podemos encontrar o tempo que ela gasta para percorrer o comprimento das placas. Portanto,
Esse tempo é exatamente o mesmo tempo que a carga gasta para percorrer, na direção , a distância , blz? Por isso, a gente vai usar esse tempo lá na expressão para daqui um pouco...
Além disso, o módulo do campo elétrico uniforme se relaciona com a diferença de potencial e a distância entre as placas paralelas da seguinte maneira:
Substituindo essas duas últimas expressões naquela do Passo 2 para , obtemos:
OK? Esse exercício é interessante porque faz um paralelo direto com o caso gravitacional do lançamento oblíquo que você viu lá na Física 1 e, da mesma maneira que lá naquele caso, a gente tem aqui também uma partícula de massa , porém carregada, descrevendo uma trajetória parabólica.