Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 22.6 - Ex. 25
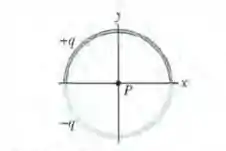
Na Fig. 22-45, duas barras curvas de plástico, uma de carga e outra de carga , formam uma circunferência de raio no plano . O eixo passa pelos dois pontos de ligação entre os arcos e a carga está distribuída uniformemente nos dois arcos. Se , determine (a) o módulo e (b) a orientação (em relação ao semieixo positivo) do campo elétrico no ponto , situado no centro da circunferência.
Passo 1
E aí, galerinha! 😁
Nesse problema temos duas barras curvas de plástico, uma de carga e outra de carga , formam uma circunferência de raio no plano . O eixo passa pelos dois pontos de ligação entre os arcos e a carga está distribuída uniformemente nos dois arcos.
Se queremos determinar o módulo e a orientação (em relação ao semieixo positivo) do campo elétrico no ponto , situado no centro da circunferência
Parece complicado? 😬
Olhe apenas para a barra de cima. O campo elétrico devido a ela tem orientação igual ao semieixo y negativo certo? Por causa da simetria, e também porque carga positiva produz campo elétrico divergente.
Agora olhe para a barra debaixo. Ela também possui orientação igual ao semieixo y negativo, pois carga negativa produz campo elétrico convergente. Então basta a gente calcular o campo devido a um dos dois arcos e multiplicar por 2 (isso só pode acontecer se os arcos tem as cargas de mesmo módulo e sinais diferentes, é o caso da questão):
Veja só! 😉
Passo 2
Item (a)
Como no caso da questão, e , substituindo na fórmula, vemos que
Tranquilo até aqui? 😁
Passo 3
Item (b)
Como vimos no passo 1, a orientação é no sentido semieixo negativo, isto é em relação ao semieixo positivo.
E aí! entendeu tudo? Responde Aí! 😊
