Iminência de Virar um Corpo
Produzido por Ludovic BeghinTeoria
Iminência de Virar um Corpo
Vamos estudar a iminência de virar um corpo. Não é nada mais do que aplicação do que vimos anteriormente.
Esse tipo de questão envolve um corpo apoiado em um suporte e é necessário aplicar as condições de equilíbrio. Imagine que tenho a situação como a figura abaixo:
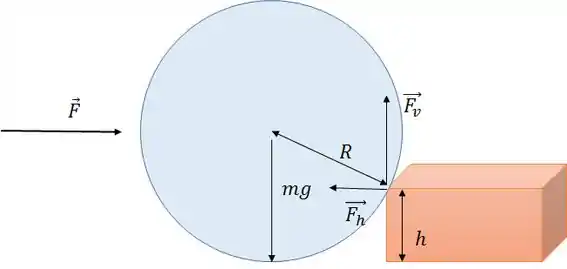
Temos uma bola apoiada em um suporte e deseja-se descobrir a força mínima necessária para virar essa bola.
Temos a força vertical e horizontal do suporte na bola. A força mg do peso da bola. O raio da esfera e uma altura do suporte.
A sacada aqui está na normal do chão. Percebeu que não colocamos?
Na iminência de virar um corpo, vamos considerar a normal do chão na esfera nula.
Mas por que?
Perceba que se a magnitude de for menor do que , a superfície na base da esfera exerce uma força normal, para cima sobre a esfera.
Se aumenta, esta força normal diminui. Logo, nesse tipo de questão precisamos determinar o valor de que manterá a esfera no lugar quando a força normal for zero, é aquele valor crítico que faz a esfera virar.
Para isso, vamos aplicar as condições de equilíbrio estável, pois o corpo ainda se encontra em equilíbrio.
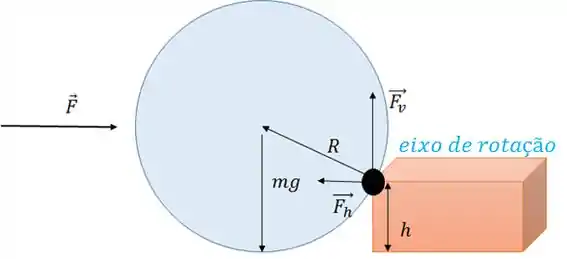
Escolha do eixo de rotação
Na hora de montarmos a equação do torque, precisamos saber escolher bem seu eixo de rotação.
Essa escolha se dá de acordo com o problema. Precisamos escolher o eixo pelo qual passa a força que não temos informações.
Assim, o torque gerado por essa força será nulo e poderemos descobrir seu valor em função das outras equações.
Nesse tipo de estão, um bom eixo de escolha é o ponto no qual o corpo se apoia para virar.
No caso do exemplo, escolheríamos o ponto de contato entre a esfera e o suporte e dessa, forma o torque gerado por e por seriam nulos.
Se liga!
Relação entre altura e raio
Na hora de aplicar , vai ser necessário achar a distância perpendicular do eixo até a linha de ação da força peso.
Para isso, você vai precisar montar uma relação entre o e . Perceba que podemos montar um triângulo retângulo com a relação entre eles.
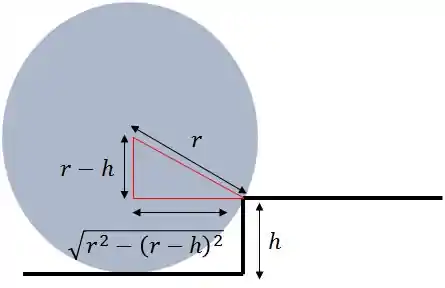
E aí? Sacou?
Parece complicado, mas é bem simples.
Apenas aplicamos a relação de Pitágoras no triângulo montado.
É isso!
Alguns problemas podem pedir a altura mínima para que seja possível virar o corpo. Mas é só aplicação dessas condições também e manipular as equações. Nesse caso, é provável que a força seja dada pelo enunciado.
Vamos para os exercícios?
Escolha do eixo de rotação
Relação entre altura e raio
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 19-21
Na figura abaixo, qual é o menor valor do módulo da força horizontal (constante) , aplicada horizontalmente ao eixo da roda, que permite à roda ultrapassar um degrau de altura ? O raio da roda é e a massa .
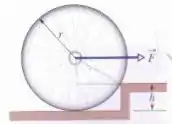
Passo 1
Primeiramente, vamos entender as forças que atuam no problema.
A gente desconsidera força normal na base da roda, porque a força mínima vai ser o ponto que essa normal é zero.
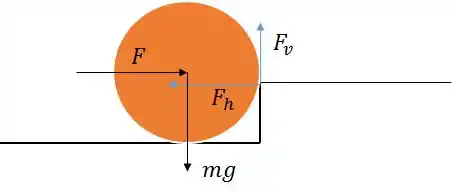
Passo 2
Sabemos que como o mínimo de força é aplicado, a roda não vai apresentar aceleração.
A força mínima é um infidesimal maior do que a força que a força que garante o equilíbrio. É como se a gente colocasse uma formiga na situação de equilíbrio e a roda andasse.
Como não tem aceleração, a força resultante é zero. E... Podemos usar as equações de equilíbrio!
Vamos calcular o torque resultante no ponto em que a roda toca na quina.
Repare só na figura.
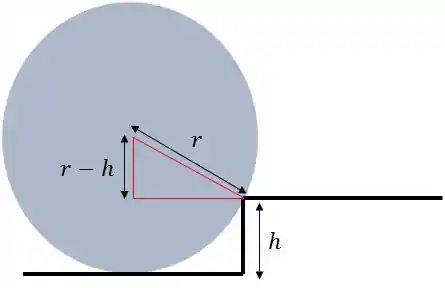
Show!
Quando calculamos o torque resultante nesse ponto, já sabemos que o torque gerado por e são nulos.
Temos que achar o torque gerado por e por .
A distância perpendicular da linha de ação de até o eixo é de .
A distância perpendicular da linha de ação de mg até o eixo é o outro cateto. Sabemos que por Pitágoras, ele vale:
Passo 3
Opa! Falta só aplicar a equação do torque. Considerando o sentido anti-horário positivo.
Podemos substituir os valores do problema.
Resposta
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 19-14
Um caixote cúbico uniforme tem de lado e pesa . Ele repousa em um piso com uma das arestas encostada em um obstáculo fixo muito pequno. A que altura mínima acima do piso deve ser aplicada uma força horizontal de para virar o caixote?
Passo 1
Primeiramente, vamos tentar entender melhor a figura:
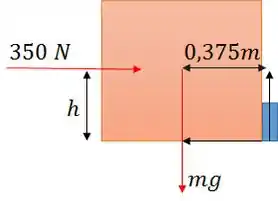
A altura mínima para virar o caixote é aquela que garante o equilíbro. Um infidesimal a mais, o caixote cúbico viraria.
Passo 2
Vamos aplicar então, as condições de equilíbrio! Sempre elas!
Escolhendo o eixo de rotação o aresta que encontra o obstáculo pequeno, podemos desconsiderar o torque gerado pela força do chão e pela força do obstáculo.
A distância perpendicular da força peso até a aresta do cubo é metade de . Vale .
A distância perpendicular da linha de ação da força aplicada até a aresta é
Convencionando o sentido anti-horário como positivo, podemos aplicar a equação do torque:
Resposta
Exercício Resolvido #3
Paul A. Tipler e Gene Mosca, Física Para Cientistas e Engenheiros Volume 1, 6ª edição, Cap 12, pp 427 - 62
Um lápis sextavado é colocado sobre um caderno (figura abaixo). Determine o menor coeficiente de atrito estático , tal que, se a capa do caderno for erguida, o lápis rolará para baixo sem escorregar.

Passo 1
Vamos montar a figura do problema.
Temos a força de atrito, a força normal e a força peso. Fica mais fácil colocar o eixo xy na direção da força de atrito e normal, porque assim já contemplamos duas forças.
Dá para fazer uma manipulação rápida ali e transferir o para a componente do peso.
O ângulo interno de um hexágono é regular é e o ângulo externo é .
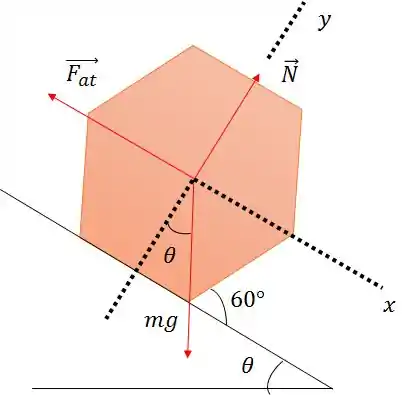
Passo 2
Na situação limite do rolamento, ainda temos as condições de equilíbrio. Isso significa que o torque resultante em relação a qualquer ponto ainda deve ser zero. Nessa situação, o lápis fica apoiado somente no ponto A, indicado na figura abaixo.
Assim, se quisermos que o lápis esteja na iminência de rolar sem escorregar, é necessário que o centro de massa esteja acima do ponto A, ou seja esse ponto e o centro de massa ligados geram uma reta vertical. Dessa forma, ao aplicarmos o torque em relação a esse ponto, ele ainda será igual a zero (já que as forças normal e atrito estarão nesse ponto e a força peso tem como direção uma reta que passa por esse ponto).
Dando um zoom para explicar isso. Olha como fica!
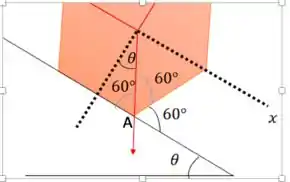
Assim, vemos que o ângulo crítico, ou seja, na iminência dele girar é de .
Se aumentássemos um pouquinho só esse ângulo, o lápis já viraria.
Passo 3
Agora, precisamos relacionar o ângulo com o coeficiente de atrito .
Vamos aplicar as condições de equilíbrio, já que como estamos falando do menor coeficiente de atrito, estamos falando, também, de iminência.
Então, aplicamos
Passo 4
Para isso, vamos decompor nos eixos e .
Passo 5
Depois de já decompomos, fica mais fácil. Se liga:
Como queremos relacionar com , precisamos colocar o coeficiente de atrito na história.
Você se lembra que ? Então, vamos usar isso aqui.
Sabemos que o ângulo crítico da iminência é .
Logo o mínimo é