Teoria
Binários
Imagine a seguinte situação.
Dois amigos, João e Lucas, decidem brincar para ver quem é mais forte. A lógica da brincadeira era simples.
Os dois iam empurrar uma geladeira em lados opostos e quem conseguisse fazer com que a geladeira andasse para o lado que empurrava, ganharia o jogo.
O problema foi que João preferia empurrar a geladeira na parte debaixo e Lucas na parte de cima, da seguinte forma:

Resultado: A geladeira quase caiu em cima de João e Lucas saiu como vencedor. Mal sabiam eles que a força aplicada por cada um tinha sido exatamente a mesma.
Você saberia explicar isso?
Vamos entender!
Vamos entender o que aconteceu através da figura abaixo:
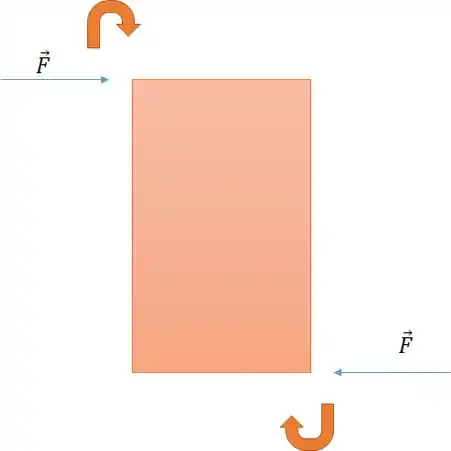
A força de João foi igual a de Lucas, então a força resultante foi zero.
Repare na figura:
A questão foi que o torque resultante não foi zero e, por isso, a geladeira quase caiu em cima do João.
Se colocássemos um eixo imaginário no centro da geladeira tanto a força do João, quanto a do Lucas tenderiam a girar a geladeira no sentido horário, como mostra a figura.
Conceito de binários
Essa é justamente a definição de binários. O binário é a ação de duas forças de mesma intensidade e sentidos opostos aplicados em pontos diferentes.
Mesmo sofrendo a ação de duas forças, o binário tende a produzir apenas uma rotação.
Tá! Mas qual o valor desse momento?
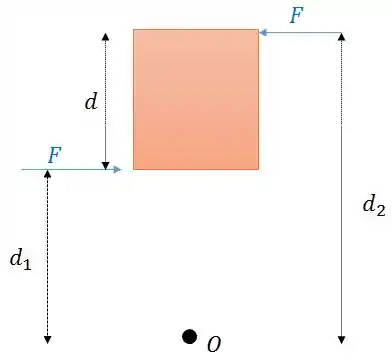
A figura acima representa um momento binário de um corpo qualquer. Vamos calcular o momento resultante desse binário em relação ao eixo , distante do corpo.
Percebemos que a força de cima tende a girar o corpo no sentido anti-horário, enquanto a força debaixo tende a girar o corpo no sentido horário.
A distância da linha de ação da força debaixo até o eixo de rotação é e a distância da linha de ação da força de cima é .
Logo, podemos aplicar o torque resultando, convencionando o sentido anti-horário como positivo.
Percebe que é exatamente o valor de , a distância entre as duas forças.
Logo,
Perceba que o momento resultante de um binário independe da posição do eixo de rotação, depende apenas do módulo das forças aplicadas e da distância entre elas.
É basicamente isso que você vai aplicar nos exercícios!
Vamos fazer?
Conceito de binários
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Duas forças de estão dispostas como na figura abaixo. Sabendo que o raio da circunferência é de , qual o torque gerado por essas forças?
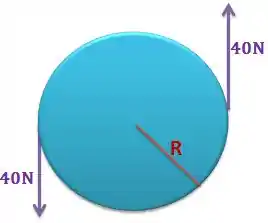
Passo 1
Questão simplérrima de binário, galera! Bora lá!
Temos na questão um binário. Sabem o porquê, né?
Duas forças de módulos iguais, na mesma direção, porém em sentidos opostos.
Passo 2
Pra calcular o torque gerado por ela aqui é só aplicar a formula que a gente já aprendeu.
Nosso a gente já sabe que é . Mas e esse aí?
Se liga nessa figura aqui.
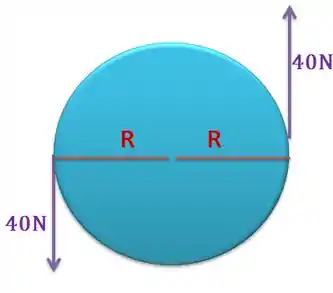
Deu pra ver quem é, né?
Desta forma podemos dizer que
Resposta
Exercício Resolvido #2
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 425 – 31.
Duas forças de são aplicadas em cantos opostos de uma placa retangular, como mostra a figura abaixo. Determine o torque produzido por este binário.
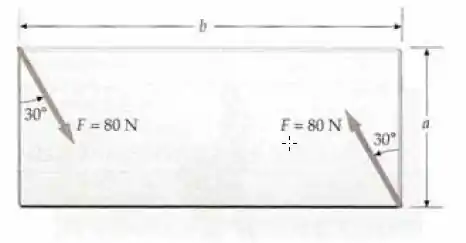
Passo 1
Vixe! Questão parece difícil, né? Mas vem comigo que a gente vai longe. ;D
Temos um binário e pra calcular o torque de um binário é simples.
A parada é que esse não é tão óbvio e aí vamos ter que usar um pouquinho de trigonometria. Bora lá?
Passo 2
Prolongando os vetores força e calculando a distância entre eles, podemos fazer esse diagrama aqui:
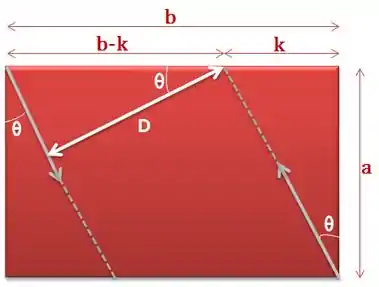
Pra achar esse aí é tranquilo, né?
Logo
Beleza. Foca agora no triângulo superior. Aquele ali do e do .
Fazendo uma relação entre justamento podemos dizer que:
Passo 3
Agora sim, é só aplicar na fórmula dos binários substituindo o por .
Fim. :}