Atrito Estático
Produzido por Ludovic BeghinTeoria
Você já teve que empurrar alguma coisa pesada, tipo um móvel, e percebeu que o mais difícil é fazer ele começar a se mover…depois fica bem mais fácil empurrar? Esse fenômeno tem TUDO a ver com atrito estático! A força de atrito é uma força que age sempre no sentido contrário ao movimento:
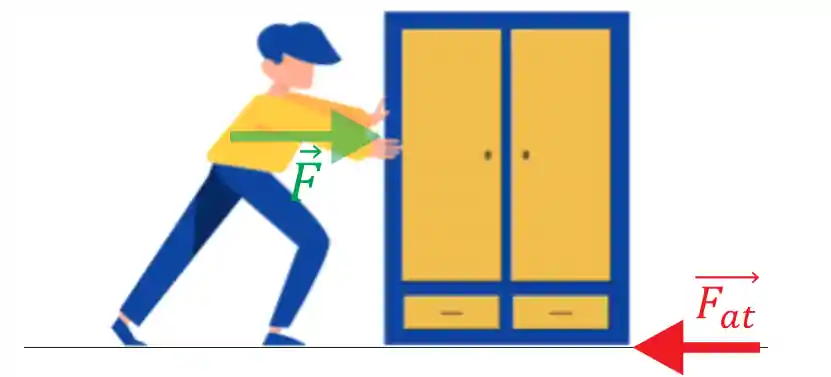
O atrito estático é aquele que a gente considera quando o objeto ainda esta parado, para que o armário ali de cima comece a se movimentar a força
📢 Clique para ver mais:
Força de Atrito Estático
Imagina que estamos querendo mover o guarda roupas da imagem acima, só que pra isso temos que vencer a força de atrito estático máximo. Como a gente pode calcular essa força?!
Para isso usamos a seguinte fórmula:
Onde
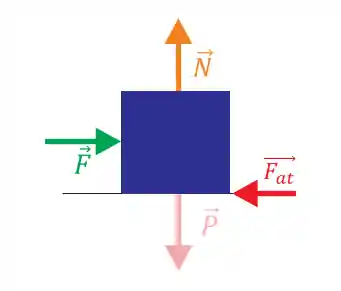
A força peso
Com o corpo parado, a única certeza que temos é que a resultante das forças, também na horizontal, é nula e, portanto:
Queremos saber a força necessária pra fazer o armário se mover, então a força de atrito é máxima:
Com isso podemos dizer que:
Agora é só calcular a força de atrito máxima e saberemos a força necessária pra fazer o objeto começar a se mover!
Você também pode conferir esse conteúdo em vídeo:
Exemplo: Uma força de
A força de atrito estático é dado por:
No equilíbrio temos:
Logo:
Substituindo:
A Fat máxima é menor que a força aplicada, então o bloco se move! Agora vamos fazer exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 141-2
Em três experimentos, três forças horizontais diferentes são aplicadas ao mesmo bloco que está sobre a mesma bancada. Os módulos das forças são e . Em cada experimento o bloco permanece estacionário, mesmo com a aplicação da força. Ordene as forças, em ordem decrescente, de acordo (a) com o módulo da força de atrito estático que a bancada exerce sobre o bloco e (b) com o valor máximo dessa força.
Passo 1
Essa é uma questão teórica e somente conceitual. Aprendemos que a força de atrito estático vai aumentando, no sentido contrário, de acordo com o aumento da força que é aplicado ao bloco. A força de atrito só pára de aumentar quando a força aplicada ultrapassa a força de atrito máxima que a bancada exerce no bloco. Vimos também que essa força de atrito máxima é dada pela fórmula:
Portanto, essa força máxima não depende do aumento da força horizontal que é aplicada ao bloco, já que, como essa força é horizontal, ela não interfere no valor da normal entre o bloco e a superfície.
Concluímos então que, as forças são iguais as forças aplicadas ao bloco e os valores é o mesmo para todas as situações.
Resposta
- Não é possível ordenar, já que possuem o mesmo valor.
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 141-3
Na Fig. 6-15, se a caixa está parada e o ângulo entre a horizontal e a força aumenta, as grandezas a seguir aumentam, diminuem ou permanecem com o mesmo valor: (a) ; (b) ; (c) ; (d) ?
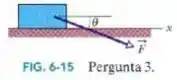
Passo 1
Temos aqui novamente uma questão conceitual, temos que analisar caso a caso. Comecemos com a letra (a).
não é nada mais do que a componente de na horizontal, então:
Como aumenta, diminui e diminui.
Passo 2
Agora, na letra (b), vamos analisar a variação de , que é a força de atrito que a superfície aplica na caixa.
Aprendemos que a nasce quando algum tipo de movimento é incentivado e vai crescendo de acordo com a intensidade da força que gera esse movimento, sempre no sentido oposto. Enquanto não há movimento, tem sempre o mesmo módulo da força horizontal aplicada. Portanto:
Se diminui, diminui.
Passo 3
Já pra letra (c) nos é pedido para avaliar a variação da força normal . Sabemos que o chão não vai furar, portanto, a força normal vai sempre responder com o mesmo módulo e com sentido contrário à componente vertical da força :
Como aumenta, aumenta.
Passo 4
Por último, analisaremos a variação de . Aprendemos que a expressão que rege o módulo da força de atrito máximo é dada por:
Como é constante e aumenta, aumenta.
Resposta
- diminui
- diminui
- aumenta
- aumenta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 141-5 – letras a,b,c,d
Se você pressiona um caixote de maçãs contra uma parede com tanta força que o caixote não escorrega parede abaixo, qual é a orientação (a) da força de atrito estático que a parede exerce sobre o caixote e (b) da força normal que a parede exerce sobre o caixote? Se empurra o caixote com mais força, o que acontece (c) com e (d) com ?
Passo 1
Primeiramente vamos fazer um desenho da situação, junto com todas as forças que atuam no caixote.
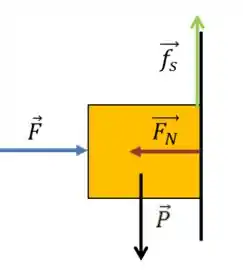
Nos foi dito que o caixote está parado, portanto, segundo a primeira lei de Newton, a força resultante tem que ser zero.
Se separarmos a análise nos eixos e , chegamos às orientações mostradas na figura acima, respondendo assim as letras (a) e (b).
Passo 2
Para responder as letras (c) e (d), temos que usar o fato de a soma das forças em cada eixo tem que ser zero. Portanto, analisando o eixo , temos:
Onde concluímos que, se aumentarmos , aumentamos também , o que responde a letra (d).
Já no eixo , temos:
é fixo e, portanto, o valor de não muda, respondendo a letra (c).
Resposta
- Vertical para cima
- Horizontal, com sentido contrário a
- Se mantém constante
- Aumenta, já que tem o módulo igual a
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 151-108
Bagagens são transportadas de um local a outro de um aeroporto por uma esteira . Em um certo local a esteira tem uma inclinação de com a horizontal. Suponha que para o ângulo tão pequeno as malas não escorreguem. Determine o módulo da força de atrito exercida pela esteira sobre uma caixa de de peso quando a caixa está na parte inclinada da esteira e a velocidade da esteira é (a) nula e constante, (b) e constante, (c) e aumentando a uma taxa de e (d) e diminuindo a uma taxa de e (e) e aumentando a uma taxa de . (f) Para quais dessas cinco situações a força de atrito é dirigida para baixo ao longo da rampa?
Considere que quando a mala sobe a sua velocidade é positiva.
Passo 1
Antes de começarmos, temos que entender o porque das esteiras conseguirem arrastar os corpos.
A situação a se comparar nesse caso é aquela que temos um bloco em cima do outro e existe uma força aplicada somente no bloco de baixo. Nesse caso, o bloco de cima só se move se houver atrito na superfície entre os dois blocos.
O que temos que fazer aqui é o de sempre: fazer o diagrama de corpo livre e aplicar a segunda lei de Newton. O importante a se perceber aqui é que como as malas não escorregam, a aceleração delas é igual à aceleração da esteira.
Passo 2
Vamos fazer o diagrama de corpo livre da situação da letra (a):
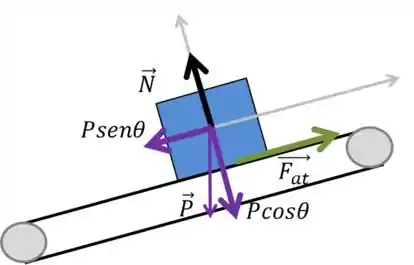
A velocidade da esteira é nula e constante, portanto, a aceleração da esteira e do bloco são nulas. Vamos portanto aplicar a segunda lei de Newton no eixo que está na direção da esteira.
Substituindo os valores de e :
Passo 3
Já para a situação da letra (b), temos que a velocidade da esteira é constante, portanto, a aceleração da esteira e do bloco são nulas. Vamos portanto aplicar a segunda lei de Newton no eixo que está na direção da esteira.
Substituindo os valores de e :
Passo 4
Na situação da letra (c), temos uma aceleração de . Considerando o eixo que colocamos na figura acima, temos então que:
Não sabemos o sentido da , mas vamos manter o diagrama com ela pra cima e, se ela der negativa, nossa suposição está errada.
Aplicando a segunda lei de Newton no sentido da esteira:
Substituindo os valores de e :
Passo 5
Na letra (d), a aceleração tem o mesmo módulo que a letra (c), mas está no sentido oposto, portanto . Aplicando a segunda lei de Newton:
Substituindo os valores de e :
Como a deu positivo, nossa suposição estava certa e ela está apontando para cima.
Passo 6
Finalmente, para a letra (e), temos a mesma coisa da letra (c), mas com um valor diferente para a aceleração que é , também para cima. Observando o sinal de menos na aceleração e aplicando a segunda lei de Newton:
Substituindo os valores de e :
Passo 7
Em nenhuma das situações a aponta para baixo.
Resposta
- Nenhuma das situações
Exercício Resolvido #5
UFRJ-Física 1-P1 2015.1 ME8
Uma força horizontal , de módulo 40 N, empurra um bloco de peso 30 N contra uma parede vertical. O coeficiente de atrito estático entre a parede e bloco é 0,80 e o de atrito cinético é 0,60. Suponha que inicialmente o bloco esteja em repouso. A sentença correta é
(a) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 32 N;
(b) O bloco começará a se mover e o módulo da força resultante exercida pela parede sobre o bloco vale 51,2 N;
(c) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 70 N;
(d) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 50 N;
(e) O bloco não se moverá e o módulo da força resultante exercida pela parede sobre o bloco vale 30 N;
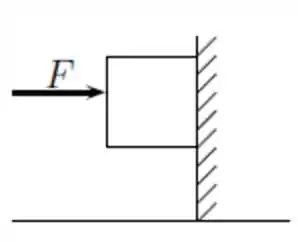
Passo 1
Vamos ver todas as forças que atuam no bloco quando ele está em repouso.
Tem a força , a força peso , e as forças exercidas pela parede, que são a normal e a força de atrito estático .
Então o diagrama de corpo livre do bloco é:
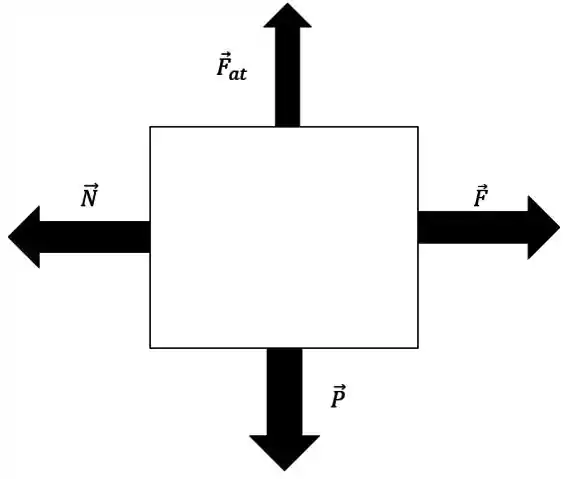
Passo 2
O bloco está em repouso, então a força resultante atuando nele é nula. Então também podemos dizer que a força resultante atuando no eixo também é nula:
E as forças agindo no eixo são a e a normal , logo:
Vou botar o módulo da normal como em vez de pra não confundir com Newton, ok?
Então ficou:
E ele deu , então
(Seria chato ficar né? rs)
Passo 3
Vamos fazer a mesma coisa no eixo . A força resultante é:
E como o bloco está em repouso:
Ou seja,
E o módulo da força peso vale , ou seja:
Passo 4
A força de atrito estático a gente só sabe calcular quando ela é máxima, quando o corpo está prestes a se mover. Então vamos assumir que o bloco está na iminência de um movimento, pra ver se a força de atrito da parede daria conta de manter o bloco em repouso.
A força de atrito estático máximo tem seu módulo dado por:
sendo o coeficiente de atrito estático. E aqui , logo:
E vimos que , então
Passo 5
Ou seja, se o bloco estivesse na iminência de um movimento, no ponto de cair, a força de atrito valeria . Ou seja, ela teria módulo maior que o do peso (), e manteria o bloco em repouso.
A força de atrito tem módulo : essa diferença de em relação à força de atrito estático máximo mostra que além do bloco não cair, nem quase caindo ele está.
Passo 6
Ainda falta definir a segunda parte da questão, da força resultante exercida pela parede sobre o bloco.
Essa força nada mais é que a soma da normal e da força de atrito. Mas não podemos simplesmente somar os módulos das forças, temos que somar os vetores!
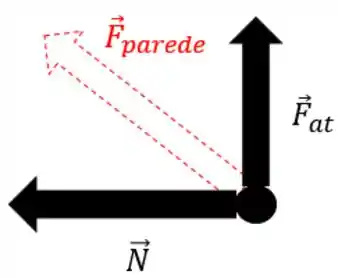
Passo 7
Sabemos que e , então pra achar só precisamos aplicar um Pitágoras básico:
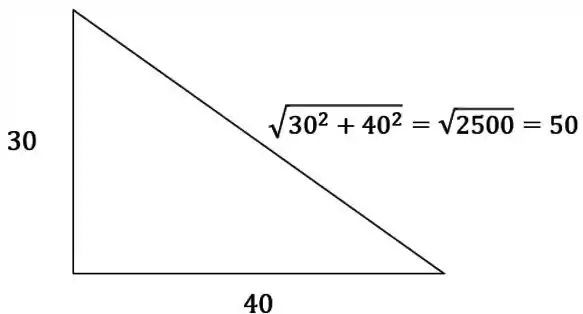
Ou seja, !
Resposta
Alternativa (d)