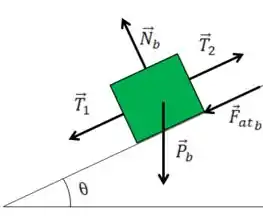
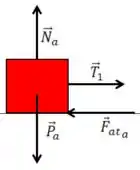
Atrito Cinético
Produzido por Ludovic BeghinTeoria
Você já teve que ajudar a fazer um carro pegar no tranco? Percebeu que o mais difícil é fazer o carro sair do lugar, depois é bem mais de boas?

O atrito cinético tem TUDO a ver com esse fenômeno! Mas antes de qualquer coisa, pra entender como o atrito cinético funciona, se liga nesse vídeo aqui! 👇
📢 Clique para ver mais:
Força de Atrito Dinâmico x Força de Atrito Estático
O atrito cinético, também chamado de atrito dinâmico é o atrito presente nos objetos que estão em movimento e ele irá sempre se opor ao sentido do movimento. Ele é dado por:
Onde
Aqui
Exemplo: Considere um bloco de massa
A força de atrito estático é dado por:
E como a gente tem o equilíbrio no eixo
Sendo assim:
Substituindo:
A força de atrito máxima é menor que a força aplicada, então o bloco começa a deslizar e possuir uma aceleração!
Agora vamos fazer mais exercícios?
Exemplo: Considere um bloco de massa onde o chão possui coeficiente de atrito estático e uma força é aplicada ao bloco. O bloco se mexe?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 142-3
Uma pessoa empurra horizontalmente um caixote de com uma força de para deslocá-lo em um piso plano. O coeficiente de atrito cinético é . (a) Qual é o módulo da força de atrito? (b) Qual é o módulo da aceleração do caixote?
Passo 1
a) O enunciado não citou o coeficiente de atrito estático, apesar de não deixar explícito que o corpo está em movimento. Consideraremos então que a força aplicada é maior que a força de atrito estático máxima, portanto, o bloco está em movimento. Sabemos que a força de atrito cinético é constante e tem fórmula definida por:
E como não há aceleração na vertical:
Substituindo uma equação na outra:
Conhecemos os valores de , e , portanto:
Passo 2
b) Para resolvermos esse item, basta aplicarmos a segunda lei de Newton.
Nos foi dado o valor de , que é aplicada horizontalmente e sabemos o valor de , que age no sentido contrário da aceleração. Portanto, substituindo os valores:
Resposta
Exercício Resolvido #2
PUCRIO-P1-B-2012.2 Q2
Um bloco de peso está deslizando para baixo em um plano inclinado de com a horizontal. Existe atrito entre o bloco e o plano. A aceleração do bloco é de dirigida para baixo ao longo do plano.
a) Desenhe o diagrama de corpo livre para o bloco durante a descida.
b) Calcule o valor do coeficiente de atrito cinético entre o bloco e o plano.
Passo 1
a)
O bloco não possui nenhuma força agindo sobre ele além da força peso e das duas forças de contato (normal e atrito).
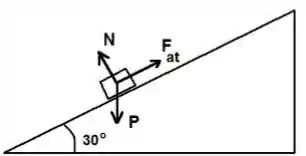
Para facilitar, escolhemos o eixo paralelo ao plano inclinado e o sentido positivo no sentido do movimento, e o eixo paralelo ao vetor da força Normal e sentido positivo no mesmo sentido da normal.
Passo 2
b)
A segunda lei de Newton neste caso fica:
Por componentes:
Eixo :
Porém . Logo:
Eixo :
Então, decompondo o peso:
Resposta
a)
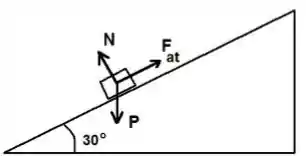
b)
Exercício Resolvido #3
UERJ-LISTA 1-16 a, b c
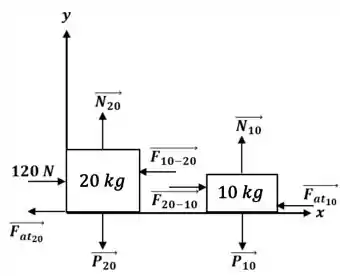
Dois blocos ( e ) são empurrados por uma força horizontal de como mostra a figura abaixo. O coeficiente de atrito entre os blocos e o solo é 0,2.

Desenhe um diagrama das forças que atuam em cada um dos blocos e as escreva em um referencial determinado por você.
Determine a aceleração do conjunto e as forças que atuam em cada bloco.
Se a posição dos blocos fosse trocada o que mudaria nas forças e na aceleração?
Passo 1
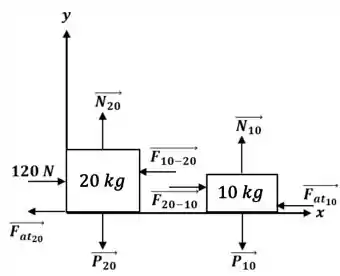
Passo 2
Vamos usar a segunda lei de Newton () para o sistema. Lembrando que o sistema não possui movimento no eixo , o peso e a normal dos blocos se anulam.
Pela terceira lei de Newton sabemos que os pares ação e reação tem o mesmo valor mas com sentidos diferentes. Portanto, , logo, elas se cancelarão no sistema, sobrando apenas.
Agora basta calcular e , vamos usar a fórmula da força de atrito ()
Como vimos no início deste item, e , portanto:
Agora podemos calcular a e a utilizando a segunda lei de Newton () para o bloco de massa igual a :
Novamente, usando para o bloco de massa igual a :
Passo 3
Mudar a posição dos blocos apenas afetará o valor das forças de ação e reação entre os blocos, mas como essas forças se cancelam no cálculo da aceleração, a aceleração será a mesma, independentemente da posição dos blocos.
Resposta
Mudar a posição dos blocos apenas afetará o valor das forças de ação e reação entre os blocos, mas como essas forças se cancelam no cálculo da aceleração, a aceleração será a mesma, independentemente da posição dos blocos.
Exercício Resolvido #4
PUCRIO-P1-B-2015.1 Q1.2
Considere a situação ilustrada abaixo onde os dois blocos estão ligados por uma corda que passa por uma polia. O bloco 1 tem massa e o bloco 2 tem massa . As massas da polia e da corda podem ser consideradas como sendo desprezíveis. Existe atrito em todas as superfícies e o coeficiente de atrito cinético é igual a 0,40. Uma força é aplicada no bloco 1 de tal forma que os blocos se deslocam com velocidade constante, o bloco 1 para à direita e o bloco 2 para à esquerda.
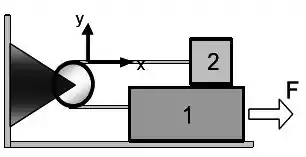
a) Faça o diagrama de corpo livre para o sistema e indique nos dois blocos, se existirem, as forças que formam pares ação-reação.
b) Escreva, na forma literal, as equações de movimento para o sistema. Resolva o sistema de equações e substitua os valores do enunciado para encontrar o vetor força . Utilize o sistema de coordenadas indicado.
Passo 1
(a)
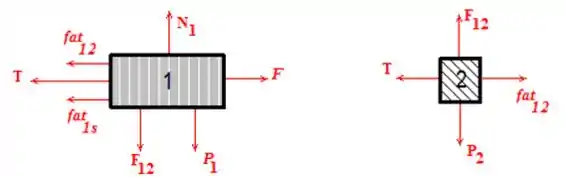
Onde representa a força de atrito entre os dois blocos que irá atuar em ambos. E é a força de atrito do bloco 1 com o solo. Além de que é a força de normal de contato entre os dois blocos.
Há três conjutos de forças em par ação e reação:
1 – força de atrito tangencial entre as superfícies do blocos 1 e 2 ()
2 – tração no fio ideal ()
3 – Força normal entre as superfícies dos blocos 1 e 2 ()
Passo 2
(b)
Aplicando a segunda lei de Newton para cada um dos dois blocos:
Bloco 1:
Bloco 2:
Como os blocos não se movem na vertical, então . Logo:
Usando a (eq.4):
Usando a (eq.2):
Entretanto, descobrimos que , então podemos substituir:
Como os blocos se movem com velocidade constante, . Desta forma:
Usando a (eq.3):
Usando a (eq.1):
Mas já sabemos que então:
Utilizando a fórmula da força de atrito:
Substituindo os valores que encontramos na eq. 2 e eq. 4:
Substituindo os dados:
Resposta
(a) 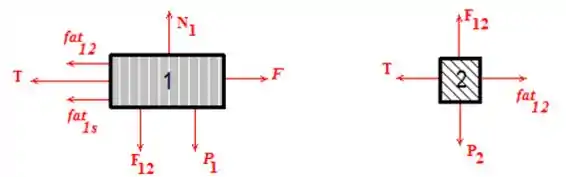
,,
(b)
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 148-69
Na Fig. 6-53, um caixote escorrega para baixo em uma vala cujos lados fazem um ângulo reto. O coeficiente de atrito cinético entre o caixote e a vala é . Qual é a aceleração do caixote em termos de , e ?
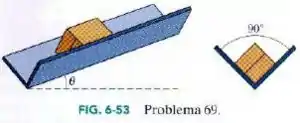
Passo 1
Temos aqui uma situação especial, onde existem duas superfícies que oferecem atrito ao movimento do corpo. Mas não fique bolado, nada mudou. Vamos fazer o diagrama de corpo livre baseado na segunda imagem apresentada no enunciado.
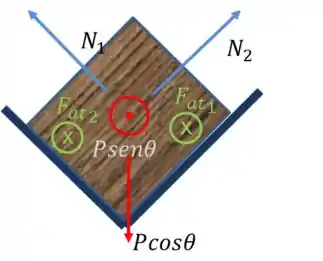
Beleza, temos todas as forças expressas no diagrama acima, mas temos agora, diferente das outras vezes, 3 eixos pra analizar. Vamos usar os seguintes eixos como referência:
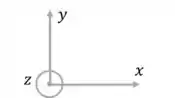
Passo 2
Temos movimento, ou seja, temos aceleração somente no eixo , portanto, podemos aplicar a primeira lei de Newton nos eixos e . Decompondo as forças e no eixo , temos:
Para facilitar, vamos chamar o valor das normais de , portanto:
Passo 3
Já no eixo , temos:
Usando o resultando obtido anteriormente:
Passo 4
Habemus movimento no eixo ! Nos foi dito que o caixote está descendo, portanto, usaremos a segunda lei de Newton:
Substituindo as expressões para o peso e para a força de atrito cinético, temos:
Resultados anteriores dizem que:
Substituindo o valor de e , portanto:
Chegamos finalmente ao valor de :
Resposta
Exercício Resolvido #6
Elaboração Própria
Os blocos , e são dispostos como indicado na figura abaixo e ligados por cordas de massas desprezíveis. A massa de e de são iguais a . O coeficiente de atrito cinético entre cada bloco e a superfície é igual a . O bloco desce com velocidade constante. a) Desenhe dois diagramas de corpo livre separados mostrando as forças que atuam sobre e sobre . b) Ache a tensão na corda que liga o bloco e . c) Qual é o peso do bloco ?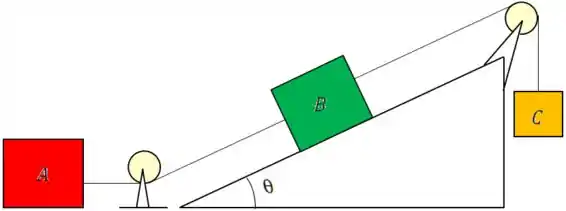
Passo 1
a)
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Sim, existe um fio.
Não, não existe mola atuando.
Sim, existe atrito.
Como o bloco está caindo isso faz com que o bloco esteja indo para direita, ou seja, a força de atrito é contraria a isso, apontando para esqueda.
Então seu DCL fica
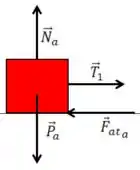
Passo 2
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com a superfície inclinada.
Sim, existe um fio.
Não, não existe mola atuando.
Sim, existe atrito.
Como o bloco está caindo isso faz com que o bloco esteja subindo o plano inclinado, ou seja, a força de atrito é contraria a isso, apontando para baixo.
Então seu DCL fica
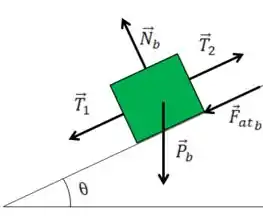
Passo 3
b)
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Agora devemos fazer o equilíbrio em cada bloco, começando pelo bloco . Vamos fazer isso porque no bloco a única força que atua no é
Como ele está com velocidade constante, ele está em equilibrio em todos os movimentos.
No
Passo 4
No
Passo 5
c)
Para acharmos o peso do bloco , devemos fazer o DCL dele.
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Não, o bloco não está apoiado em nenhuma superfície.
Sim, existe um fio.
Não, não existe mola atuando.
Não, não existe atrito.
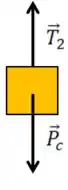
Como ele está com velocidade constante, ele está em equilíbrio em todos os movimentos.
No
Então para acharmos o peso de , devemos achar . Para isso vamos fazer o equilíbrio do bloco . Vamos primeiro fazer o DCL como normalmente escrevemos para plano inclinado.
Passo 6
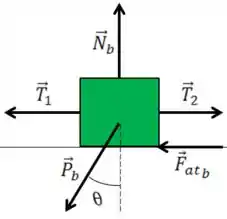
Passo 7
No
Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.
Passo 8
No
Devemos encontrar a sua componente horizontal usando a “regra do COlado, SEparado”.
Passo 9
Teremos então
Resposta