Força de Tração
Produzido por Ludovic BeghinTeoria
Seja muito bem vindo ao Responde Aí! Bora aprender como resolver problemas envolvendo Força de Tração?!
O que é tração?
A tração é uma força exercida sobre um corpo, ou um sistema de corpos, por meio de fios, cordas ou cabos.
Como Calcular a Força de Tração?
Existe uma infinidade de problemas envolvendo tração! No vídeo abaixo a gente te ensina tudo o que você precisa saber sobre força de tração para arrasar na prova de Física!
Ou se você preferir, continua comigo no textinho! 👇
Tração entre corpos do mesmo sistema
Em alguns problemas você pode encontrar dois corpos conectados sendo puxados pelo mesmo fio. Assim:

Dizemos que esses corpos fazem parte de um mesmo sistema. Mas como podemos calcular a tração do cabo que esta puxando o corpo
Vamos entender com um exemplo!
Suponha que o bloco
A chave pra resolver esse tipo de problema é fazer o diagrama do corpo livre para cada bloco, isso é, desenhar cada bloquinho isolado e olhar que tipo de força tá agindo neles.
Vamos começar com o bloco
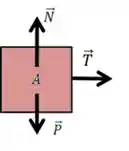
O corpo A não está quicando e nem perfurando o chão, certo? Então a aceleração do bloco A está somente na horizontal. Portanto, usando a segunda lei de Newton com o sentido positivo para a direita:
Agora vamos fazer o diagrama do corpo livre para o bloco
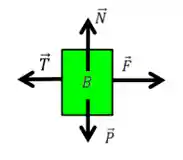
O bloco
Quando puxamos dois blocos com uma corda, esses dois blocos andam juntos, certo? Então é razoável dizer que
Com isso podemos fazer:
Isolando a tração, temos:
Substituindo os valores:
Calculamos a tração, agora só falta a aceleração:
Lembrando que
Prontinho!
Tração e força de atrito
A força de atrito
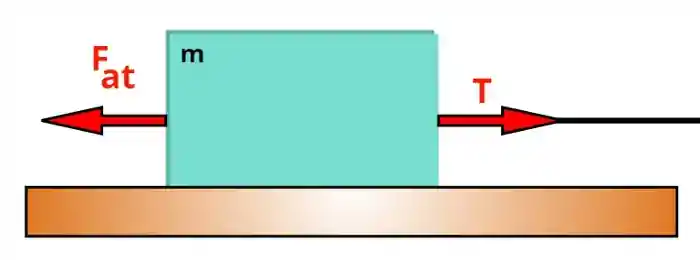
Na figura acima temos um corpo de massa
A diferença é que agora vamos considerar o atrito! Mas não se assuste, esse tipo de problema não é tão diferente do anterior.
Para calcular a tração de um cabo, considerando a força de atrito, fazemos:
A força de atrito pode ser calculada de duas formas diferentes:
- Se o bloco estiver parado, usamos o atrito estático
- Se o bloco estiver em movimento, usamos o atrito dinâmico
Tração no plano inclinado
No plano inclinado temos uma superfície onde a altura inicial é diferente da altura final, formando assim um ângulo
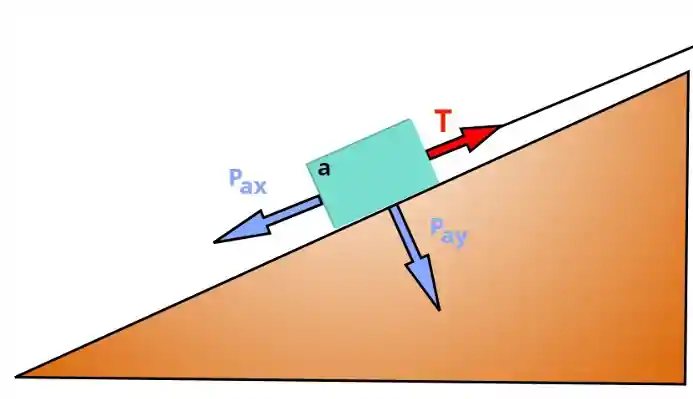
Na figura acima podemos observar um bloco de massa
Agora, como poderíamos calcular a tração do cabo?
A primeira coisa que precisamos fazer é o equilíbrio de forças que estão atuando no bloco:
O pulo do gato para resolver esse tipo de questão é fazer a decomposição das forças:
Daqui pra frente é só aplicar a Lei de Newton para achar a tração e a aceleração do bloco, caso ele esteja em movimento!
Tração no pêndulo
Um pêndulo simples é um sistema composto por um corpo de massa
IMAGEM DE UM PENDULO
Para calcular a tração no fio de um pêndulo simples, usamos a seguinte fórmula:
Onde
Agora que você já sabe como calcular a força de tração em vários sistemas diferentes, vamos praticar com exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-Física 1-P1 2014.1 ME5
Dois fios ideais e estão presos a um teto horizontal e a uma parede vertical nos respectivos pontos e , como indica a figura. Na extremidade comum dos fios está suspenso e em equilíbrio um bloco de peso . O fio é perpendicular à parede e o fio faz um ângulo com o teto . O módulo da tensão no fio é igual a
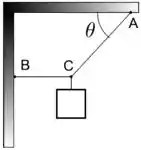
Passo 1
Vamos começar o problema fazendo DCL do bloco
Temos os seguintes dados do enunciado
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Não, ele não está apoiado em nenhuma superfície.
Sim, existem dois fios atuando.
Não, não existe mola atuando.
O DCL do bloco fica
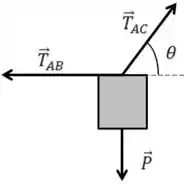
Repare que o ângulo do fio é com a horizontal, na parte de baixo ele é o ângulo do fio com a vertical.
Passo 2
Vamos fazer a analise das forças no porque é o eixo que a tração que ele procura está. Vamos ter
Devemos encontrar usando a “regra do COlado, SEparado”.
Resposta
Letra E
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 118-15
A Fig. 5-36 mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas (a) do disco A, (b) do disco B, (c) do disco C e (d) do disco D?
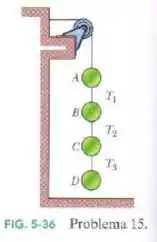
Passo 1
Temos aqui um sistema em repouso, portanto, a aceleração de qualquer corpo que pegarmos para analizar será nula.
Vamos pensar juntos: Se pegarmos qualquer um dos discos para analisar, ou seja, fazer o diagrama de corpo livre, teremos duas trações agindo nele, além da força peso. Exceto no disco D, onde temos somente uma tração. Como todas as trações estão definidas no enunciado, a única incógnita fica sendo a massa de cada disco.
Passo 2
Vamos então fazer o diagrama de corpo livre de cada disco:
No disco A:
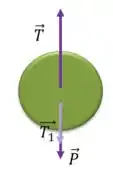
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 3
- No disco B:
- No disco C:
- Do disco D:
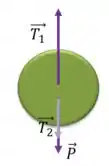
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 4
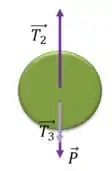
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de e de , portanto, usando :
Passo 5
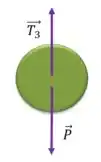
Como o corpo está em repouso, a resultante das forças deve ser nula.
Sabemos o valor de , portanto, usando :
- ''Resposta
Exercício Resolvido #3
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 121-50.
A Fig. 5-48 mostra quatro pinguins que estão sendo puxados sobre o gelo muito escorregadio (sem atrito) por um zelador. As massas de três pinguins e a tensão em duas das cordas são e . Determine a massa do pinguim , que não é dada.
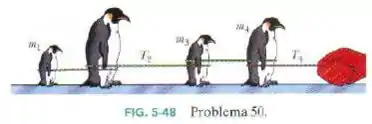
Passo 1
Vamos primeiramente juntar os dados que temos:
- Algumas das forças aplicadas em cada pinguim;
- Massas dos pinguins (exceto um).
E agora as informações que concluímos do problema:
- As cordas são inextensíveis, portanto, o deslocamento dos pinguins devem ser iguais;
- Deslocamentos iguais implicam em acelerações iguais;
- Os pinguins se movimentam somente na horizontal.
Temos então relação entre forças, massas e aceleração, podemos usar a segunda lei de Newton no diagrama de corpo livre de cada pinguim. Nos próximos passos os pinguins se tornarão, como qualquer coisa na Dinâmica, blocos. Como só vamos analisar o movimento horizontal, incluiremos no diagrama somente as forças horizontais.
Passo 2
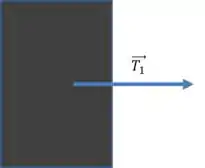
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de e :
(Eq. 1)
Passo 3
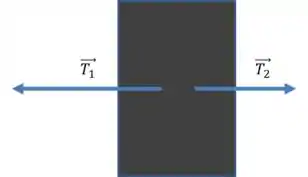
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de e :
(Eq. 2)
Passo 4
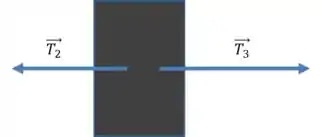
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de :
(Eq. 3)
Passo 5
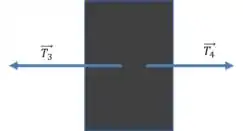
No pinguim de massa :
Usando a segunda lei:
Substituindo os valores de :
(Eq. 4)
Passo 6
Somando todas as equações, de 1 a 4, obtemos:
(Eq.5)
OBS.: A equação acima mostra como podemos encarar o conjunto de pinguins como um único corpo. A única força externa do sistema é .
Deixa esse resultado guardado por um segundo.
Agora, observando bem as equações podemos ver que se somarmos as Eqs 1 e 2 teremos como achar a aceleração:
Substituindo na Eq. 5, temos:
Resposta
Exercício Resolvido #4
UFRJ-Física 1-P1 2013.2 ME1
Três macacos , e , de mesmo peso, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. A partir de um dado instante o macaco sobe em seu cipó com velocidade constante, o macaco sobre no seu com aceleração para cima constante e o macaco desce no seu com aceleração para baixo constante. Supondo que os cipós sejam fios ideiais (inextensíveis com massa desprezível), que os movimentos se processem na vertical, que as acelerações mencionadas não sejam nulas, e denotando por , e as tensões nos cipós dos respectivos macacos , e , podemos dizer que
Passo 1
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças que atuam em cada macaco
- A massa dele é considerada?
- Ele esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Não, ele não está apoiado a nenhuma superfície.
Sim, existe fio atuando.
Não, não existe mola atuando.
O seu DCL ficará:

Passo 2
Em todas as situações, devemos lembrar atentamente o sinal dos movimentos. A equação da força resultante em todas elas ficará
Passo 3
Para o macaco
Passo 4
Para o macaco
Passo 5
Para o macaco
Passo 6
Como é positivo, temos
Resposta
Letra D
Exercício Resolvido #5
Halliday 9° edição vol.1 cap.5 seção 7 questão 16
Alguns insetos podem se deslocar pendurados em gravetos. Suponha que um desses insetos tenha massa m e esteja pendurado em um graveto horizontal, como mostra a figura abaixo, com um ângulo . As seis pernas do inseto estão sob a mesma tensão e asseções das pernas mais próximas do corpo são horizontais.
a) Qual é a razão entre a tensão em cada tíbia (extremidade da perna) e o peso do inseto?
b) Se o inseto estica um pouco as pernas, a tensão nas tíbias aumenta, diminui ou continua a mesma?
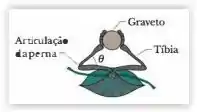
Passo 1
Vamo nessa! Bom, a gente viu no enunciado que o inseto tem 6 pernas e a componente vertical da tração em cada perna , como podemos ver na imagem , é , sendo . Aplicando a Segunda Lei de Newton à componente vertical das forças envolvidas, vemos que, para que a aceleração seja zero na direção vertical, devemos ter :
O que nos dá :
Passo 2
Como o ângulo é medido em relação à horizontal, quando o inseto “estica as pernas” o ângulo aumenta (se aproxima de ), o que faz aumentar (se aproximar de); em consequência, diminui , como vimos na fórmula achada no item anterior.
Resposta
- diminui.
Exercício Resolvido #6
UFPE 1ºEE 2017.1
A figura ao lado ilustra uma viga homogênea de peso P. A viga está sustentada na posição horizontal por uma dobradiça e por um cabo, que forma um ângulo em relação à direção da viga, como ilustrado ao lado. Quais são o módulo e o sentido da força horizontal que a dobradiça exerce sobre a viga?
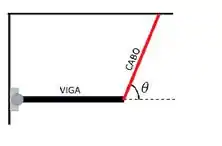
a)
b)
c)
d)
e)
f)
g)
h)
i) 0
Passo 1
Vamos primeiro olhar nosso diagrama de forças:
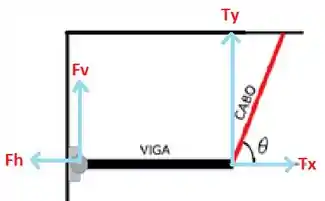
Chamando a tensão na corda de T, nós vamos ter:
E ainda teremos o peso ali no centro de massa da barra.
O equilíbrio de forças verticais vai ficar:
E o equilíbrio de forças horizontais:
Ali na decomposição das forças já te dei spoiler da orientação de né, que é o que queremos descobrir. Já sabemos então que é para a esquerda, vamos descobrir o módulo dela agora.
Passo 2
Ó, eu vou fazer o somatório dos momentos com relação à extremidade direita da barra. Isso vai me dar mais uma equação pra ajudar a resolver o problema:
Show! Agora vamos substituir:
Agora vamos voltar laaaaa em Fh:
E pra esquerda, então a setinha tem que tá assim:
Resposta
Letra H.