Plano Inclinado
Produzido por Ludovic BeghinTeoria
No plano inclinado temos uma superfície onde a altura inicial é diferente da altura final, formando assim um ângulo
O que é um Plano Inclinado?
Pra identificar um plano inclinado é muito simples! Ele é uma superfície plana, como o próprio nome sugere, que forma um ângulo
Ao estudar plano inclinado estamos muito interessados em entender como funciona o movimento de um objeto nessa superfície.
A principal novidade que vamos apresentar hoje é como fazer a decomposição das forças que atuam em um objeto se movimentando em um plano inclinado. Isso vai ser essencial na hora de resolver exercícios!
Se liga como vai ficar a decomposição de forças pro nosso exemplo:
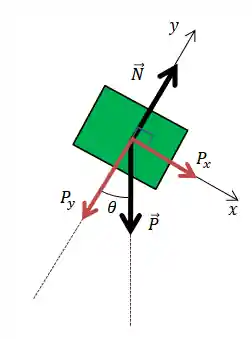
Não se assusta! A gente vai aprender como decompor as forças e resolver problemas envolvendo plano inclinado! 🤩
Aceleração no Plano Inclinado
Bora aprender na prática?!
Como encontrar a aceleração do sistema abaixo, se o bloco possuir massa
O principal pulo do gato aqui é saber utilizar os eixos cartesianos pra facilitar a nossa vida! Assim:
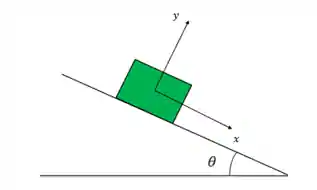
No nosso exemplo, o bloco é solto no plano inclinado que possui inclinação dada pelo ângulo
Se formos parar pra prever o movimento, a única coisa que sabemos é que o bloco não vai saltar do nada, e nem vai entrar no plano inclinado, então concluímos que a única aceleração do bloco está na direção do plano inclinado. Assim:
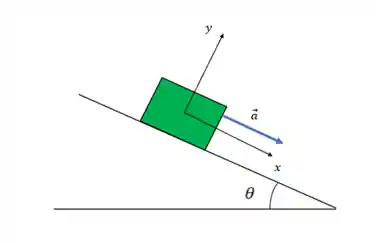
Se a única aceleração do bloco está na direção do plano inclinado, então podemos dizer que:
Nosso próximo passo é fazer o diagrama de corpo livre do bloco. Onde, o peso estará apontando para o centro da terra e a normal estará perpendicular à superfície do plano inclinado.
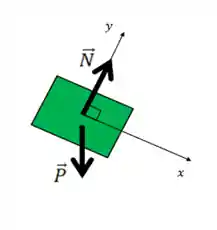
O enunciado do problema não menciona atrito, então, consideramos que não existe atrito entre o plano inclinado e o bloco.
-Mas se existisse atrito?!
Nesse caso, precisaríamos adicionar uma força de atrito
Voltando ao nosso problema, vamos decompor as forças atuantes no bloco, é como se a gente tivesse fazendo uma “conversão” dessas forças pro nosso eixo escolhido:
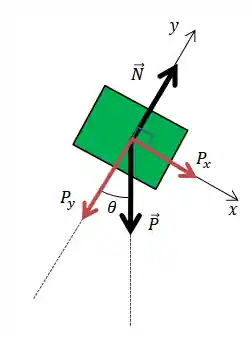
A gente não conhece nem
Então a gente precisa relacionar
Utilizando a segunda lei de newton, podemos escrever:
Mas como falamos lá em cima, a aceleração em
Cortando as massas:
Finalmente podemos calcular a aceleração:
Prontinho! 🤩
📢 Clique para ver mais:
Plano Inclinado - Vídeo Aula
Ficou com alguma dúvida?! Confere então essa vídeo aula com tudo o que você precisa pra resolver todos os exercícios de plano inclinado! 🤩
Bora praticar com mais exercícios?!
Aceleração no Plano Inclinado
Plano Inclinado - Vídeo Aula
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Um bloco de massa , está apoiado em um plano inclinado, que possui um ângulo com a horizontal. Sabendo que o bloco desliza sem atrito pelo plano inclinado, determine o módulo da aceleração do bloco e o valor da força normal que a superfície faz nele. Considere que o módulo da aceleração da gravidade é .
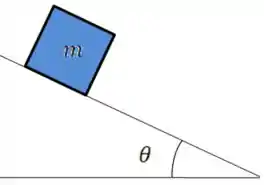
Passo 1
Temos os seguintes dados do enunciado
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
O DCL do bloco fica
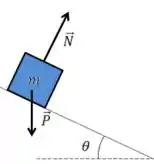
Quando temos um exercício de plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação à superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície. O DCL ficaria
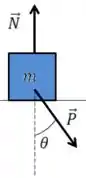
O ângulo fica na força peso com a vertical quando fazemos isso.
Passo 2
No , temos apenas a componente da força peso atuando
Devemos encontrar usando a “regra do COlado, SEparado”.
Passo 3
No temos equilíbrio das forças, tendo
Devemos encontrar usando a “regra do COlado, SEparado”.
Resposta
Exercício Resolvido #2
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 119-32
Na Fig. 5-41, um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito () com velocidade constante. Quais são os módulos de e (b) da força que a rampa exerce sobre o caixote?
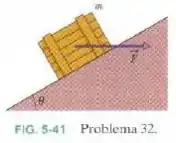
Passo 1
Para facilitar a análise do movimento mais facilmente, vamos estuda-lo nos dos eixos especiais: na direção do plano e perpendicularmente ao plano. Inicialmente as forças atuantes são essas aqui:
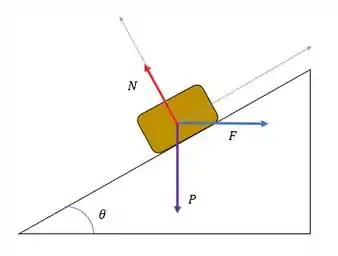
Decompondo as forças nos eixos especiais temos:
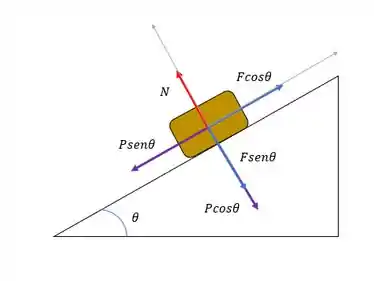
Uma parte importante do enunciado é que a caixa sobe a rampa com velocidade constante, ou seja, a resultante das forças na direção do plano é nula.
Passo 2
Vamos agora fazer o equilíbrio das forças no eixo paralelo ao plano já que é o que tem menos componentes e será mais fácil da gente analisar:
Vamos isolar a força
Onde a força peso é:
Como , podemos encontrar a força substituindo:
Passo 3
Agora que sabemos o valor de podemos encontrar a força normal ao plano fazendo o somatório das forças pro eixo perpendicular ao plano:
Substituindo os valores que a gente já calculou temos:
Resposta
Exercício Resolvido #3
UNICAMP-P1-2014.1B-Q14
Uma caixa está em repouso em um plano inclinado, sem deslizar, conforme a figura. Se aumentarmos continuamente o ângulo de inclinação do plano (medido a partir da horizontal), o módulo da força normal:
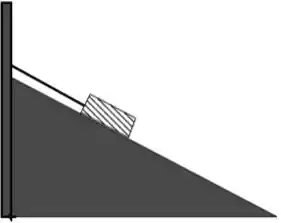
a) decresce de forma não linear.
b) não muda.
c) decresce linearmente.
d) aumenta de forma não linear.
e) aumenta linearmente.
Passo 1
Se decompusermos a força peso nessa caixa, ficaremos com a seguinte figura:
Onde:
Visto que a caixa está em repouso, a força resultante sobre a caixa tem que ser nula, portanto:
Logo:
Vamos agora ver o que acontece com a normal se aumentarmos o valor de .
O permanece o mesmo, mas o se altera, e sabemos que aumentando o ângulo, o cosseno fica cada vez menor, até chegar em , onde o cosseno será zero e portanto não haverá mais força normal. Logo, aumentando o ângulo, a força normal diminui.
Agora, analisando as alternativas ainda ficamos em duvida entre duas.
Alternativa : decresce de forma não linear.
Alternativa decresce linearmente.
Então precisamos saber o que diabos significa decrescer de forma linear ou não linear.
Vou dar alguns exemplos:
A função:
É uma função linear, porque se dobrarmos o , iremos automaticamente dobrar o , isso que significa linearidade.
Diferente da função:
Está é uma função não linear, pois se dobrarmos o , não iremos dobrar o , pois:
Voltando ao nosso problema, temos:
Onde o está envolvido com o cosseno que como acabamos de ver é não linear. Logo, ao aumentarmos o , a força normal irá decrescer não linearmente.
Resposta
Alternativa .
Exercício Resolvido #4
UNICAMP-P1-2015.1-Q12
Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado.
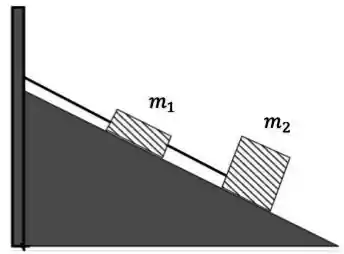
A tração medida na corda que liga o bloco de massa à parede é três vezes maior que a tração que liga o bloco ao bloco . É correto afirmar que a razão entre as massas vale:
Passo 1
Primeiro vamos desenhar as forças que atuam em cada corpo:
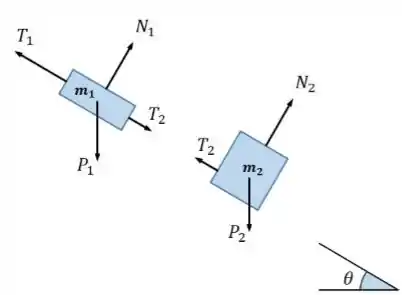
Sabemos que na direção paralela ao plano inclinado ocorre o equilíbrio das forças. Escolhendo um eixo paralelo ao plano e no sentido de subida do plano, podemos aplicar a segunda lei de Newton para o bloco 1:
Para o bloco 2:
Agora encontrando a razão :
Resposta
Letra (b)
Exercício Resolvido #5
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 122-68
A Fig. 5-60 mostra parte de um teleférico. A massa máxima permitida de cada cabina com passageiros é de . As cabinas que estão penduradas em um cabo de sustentação, são puxadas por um segundo cabo ligado à torre de sustentação de cada cabina. Suponha que os cabos estão esticados e inclinados de um ângulo . Qual é a diferença entre as tensões de partes vizinhas do cabo que puxa as cabines se as cabinas estão com a máxima massa permitida e estão sendo aceleradas para cima a .

Passo 1
Nesse exercício, para reforçar mais ainda a ideia de usar os eixos na direção do movimento e perpendicular a ele, as trações, que constituem nosso objetivo, também estão na direção do movimento. Fazendo as decomposições na direção do movimento, já que as componentes no eixo normal não são interessantes para nós, temos:
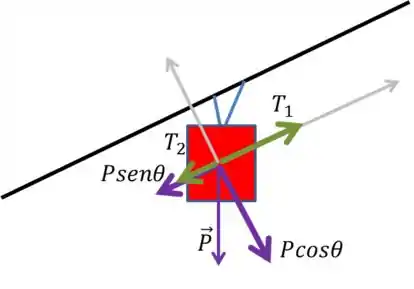
Passo 2
Foi dada a aceleração das cabines, a massa delas e nós já temos as forças que agem na direção da aceleração, agora é só aplicar a segunda lei de Newton!
Substituindo os valores conhecidos:
E então:
Passo 3
Aí você me pergunta: Mas só foi calculada a diferença entre as trações da cabine do meio, não?
A resposta é: Sim. Fizemos a análise do movimento de somente uma cabine, mas, se formos fazer das outras, perceberemos que é idêntico. As cabines possuem as mesmas massas, sofrem ação de forças de mesma direção e ainda estão sob a mesma aceleração. Portanto, a resposta encontrada para uma cabine pode ser generalizada.
Resposta
Exercício Resolvido #6
UFF-P1-2014.2-5Q
Um cunha de peso e ângulo está sobre uma superfície horizontal sem atrito. Um bloco de peso é posto sobre a cunha e uma força horizontal é aplicada na cunha (veja a figura). Também não há atrito entre o bloco e a cunha. Qual deve ser o módulo de se queremos que o bloco permaneça a uma altura constante acima da superfície horizontal?
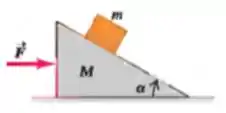
Passo 1
Antes de tudo, diagrama das forças no sistema.
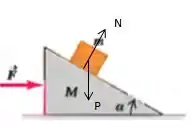
Passo 2
Normalmente, a gente decompõe as forças na direção paralela e perpendicular à rampa...
PORÉM, nesse caso queremos descobrir uma força que atua na horizontal, para isso, precisamos descobrir a aceleração do bloco na direção dessa força (horizontal).
Então, diferente do que estamos acostumados para um plano inclinado, vamos decompor as forças nos eixos padrões, (horizontal) e (vertical):
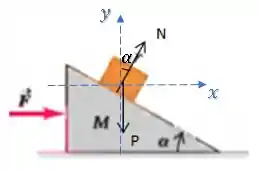
Assumindo que o corpo não se mexe verticalmente, no eixo temos:
E no eixo :
Se dividirmos uma equação pela outra vamos ter
Como
Ou seja, o módulo da aceleração correspondente à força é igual à aceleração da gravidade.
Passo 3
Olhando para o sistema, a força resultante sobre o plano e o bloco é
Como já sabemos
Os dois termos na direita são os pesos do bloco e do plano que foram dados no enunciado, assim