Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 5.Problemas - Ex. 9
09. Use o operador para obter a condição de contorno na interface entre dois meios quando existe sobre ela uma distribuição de carga com densidade superficial . Aplique o resultado a um condutor perfeito.
Passo 1
Fala aí! Vamos para mais uma?
Então, esse problema é puramente eletromagnetismo, então teremos que usar nossos conhecimentos dessa área para encontrar essa condição de contorno pedida no enunciado.
Para encontrar essa condição de contorno vamos supor dois meios onde temos uma densidade superficial de carga, como foi falado no enunciado, então temos isso aqui.
Vamos trabalhar com a eletrostática já que temos uma densidade superficial de carga.
Agora podemos imaginar um vetor de deslocamento passando de um lado para o outro e nada nos impede de usarmos a lei de Gauss para a seguinte volume:
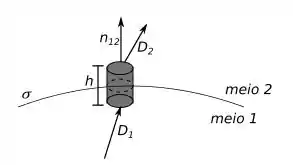
Onde , a lei de Gauss diferencial nos diz que:
Onde é a densidade de carca volumétrica.
Passo 2
A lei de Gauss bem dizer nos diz o fluxo do campo em uma superfície que nada mais é que o campo perpendicular a superfície que ele passa vezes a área dessa superfície, então tomando o limite em que tende a zero de tal forma que o fluxo pelas laterais do cilindro seja desprezível.
Temos que:
Isso significa que o fluxo do meio dois menos o fluxo do meio um é igual a carga interna.
Essa carga interna como foi a zero é igual a carga na superfície pontilhada mostrada na figura.
Como temos uma densidade superficial de carga, a carga vai ser igual a densidade superficial de carga vezes essa área, assim:
Com isso temos que:
Passo 3
Nós sabemos que
Com isso temos que:
Prontinho, encontramos a condição de contorno.
Passo 4
Agora para o caso de um condutor perfeito temos que lembrar que o campo dentro de um condutor é nulo, então no nosso caso temos que .
Assim ficamos com:
Resposta
Condição de contorno:
Condição de contorno no caso de um condutor perfeito: