Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 17.Problemas Adicionais - Ex. 94
Em de julho de , um bloco de granito se desprendeu de uma montanha no vale de Yosemite, e depois de deslizar pela encosta, foi lançado em uma trajetória balística. As ondas sísmicas produzidas pelo choque do bloco com o solo foram registrados por sismógrafos a mais de de distância. Medições posteriores mostraram que o bloco tinha uma massa entre e e que caiu a uma distância vertical de e a uma distância horizontal de onde foi lançado. (O ângulo de lançamento não é conhecido). Estime a energia cinética do bloco imadiatamente antes do choque com o solo.
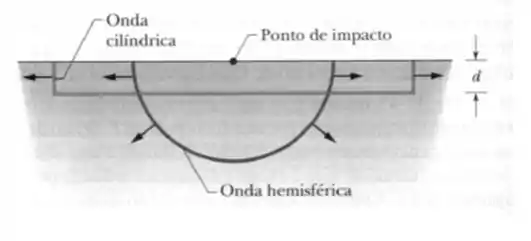
Dois tipos de ondas sísmicas devem ter sido produzidas no solo pelo impacto: uma onda volumétrica , na forma de um hemisfério de raio crescente, e uma onda superficial, na forma de um cilindro estreito. (Veja figura abaixo) Suponha que o choque tenha durado e o cilindro tinha uma altura de e que cada tipo de onda tenha recebido da energia que o bloco possuía imediatamente antes do impacto. Desprezando a energia mecânica perdida pelas ondas durante a propagação, determine a intensidade da onda volumétrica e da onda superficial quando chegaram a um sismógrafo situado a de distância. Com base nesses resultados, qual das duas ondas pôde ser detectada com mais facilidade por um sismógrafo distante?
Passo 1
A energia cinética pode ser determinada a partir da conservação de enrgia mecânica. Toda energia potencial será convertida em energia cinética, e admitindo o maior valor da massa, assim:
Considerando o melnor valor de massa teremos:
Assim a energia cinética entava entre
Passo 2
Vamos determinar quanto de energia cada onda obteve.
E a potência do pulso é determinada dividindo o valor da energia pelo tempo do choque. Assim temos:
Passo 3
A onda volumétrica se comporta como uma fonte isotrópica, sendo assim a intenidade é dada pela razão da potência pela área. Se o raio é , a área vai ser uma meia esfera e a potência foi determinada no Passo , temos:
Passo 4
A onda superficial vai se comportar também como uma fonte isotrópica, mas agora a superfície é a área lateral de um cilindro. A intensidade da onda é dada pela potência média:
A potência é a mesma, pois o pulso é o mesmo, mas a área é diferente:
Passo 5
Com isso podemos ver que a onda cilíndrica tem duas ordens de grandeza a mais que a onda volumétrica, sendo de mais fácil deteção.
Certo? Vamos pra próxima?