Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 6.Problemas Adicionais - Ex. 104

104- Um trenó para quatro pessoas (massa total = 630 kg) desce um trecho retilíneo no alto de uma encosta. O trecho retilíneo tem 80,0 m de comprimento e uma inclinação constante de 10,2° com a horizontal. Suponha que o efeito combinado do atrito e do arrasto do ar produz sobre o trenó uma força constante de 62,0 N para cima, paralela à encosta. Responda às perguntas a seguir usando três algarismos significativos. (a) Se a velocidade do trenó no início da reta é 6,20 m/s, quanto tempo o trenó leva para chegar ao final da reta? (b) Suponha que os ocupantes reduzam os efeitos do atrito e do arrasto do ar para 42,0 N. Para a mesma velocidade inicial, quanto tempo o trenó agora leva para descer o trecho retilíneo?

Passo 1

O sistema de forças no trenó enquanto desce a encosta é tal que:

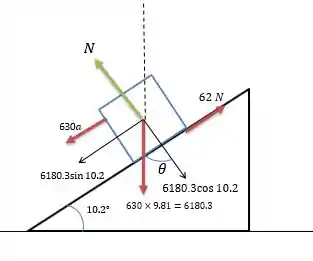
A aceleração do sistema pode ser encontrada fazendo a resultante das forças no sentido paralelo a encosta.

6180.3 sin ⁡ 10.2 - 62 = 630 a

Logo:

a = 1.639   m / s 2

Passo 2

Agora para encontrar o tempo de viagem do trenó teremos que aplicar a seguinte fórmula:

s = v 0 t + a t 2 2

Onde s = 80   m e v 0 = 6.2   m / s :

80 = 6.2 t + 1.639 2 t 2

0.82 t 2 + 6.2 t - 80 = 0

Por Bháskara encontraremos como raízes:

t 1 ; t 2 = ( - 14.357 ; 6.796 )

Como somente podemos ter o tempo positivo então temos:

t = 6.796   s

Como só pode 3 algarismos significativos então:

t = 6.8   s

Passo 3

Para a letra b a única diferença é que a força de atrito total fica igual a 42 N, logo fazendo da mesma forma que foi feita no passo anterior temos que a força resultante no sentido paralelo a encosta será igual a:

6180.3 sin ⁡ 10.2 - 42 = 630 a

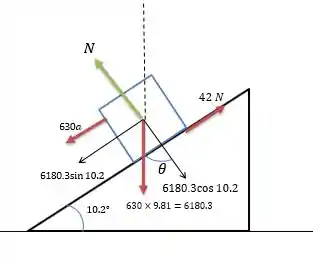
Logo a aceleração total do trenó será:

a = 1.67   m / s 2

Passo 4

Os valores de s e v 0 não mudam então:

s = v 0 t + a t 2 2

80 = 6.2 t + 1.67 2 t 2

0.835 t 2 + 6.2 t - 80 = 0

Por Bhaskara encontramos:

t 1 ; t 2 = ( - 14,18 ; 6.76 )

O valor positivo de t com três algarismos significativos será:

t = 6.76   s

Resposta

a )   6.8   s

b )   6.76   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um objeto que se move em um líquido experimenta uma força de arraste linear: D = (bv, sentido oposto ao movimento), onde b é uma constante chamada coeficiente de arraste. Para uma esfera de raio R, o
Considere um paraquedista que pulou de um helicóptero e está caindo pelo ar. Antes de alcançar velocidade terminal e bem antes de abrir seu paraquedas, sua velocidade aumenta,diminui, oupermanece cons
Quando um pingo de chuva cai pela atmosfera, sua velocidade inicialmente muda conforme ele cai em direção à Terra. Antes que o pingo de chuva atinja sua velocidade terminal, o módulo de sua aceleração
Suponha que a força resistiva que atua sobre um patinador de velocidade seja proporcional ao quadrado da sua velocidade v e seja dada por f=– k m v 2 , em que k é uma constante e m , a massa do patina
Estime a velocidade terminal de uma esfera de madeira (densidade 0,830g / c m 3 ) caindo pelo ar, considerando seu raio como 8,00c m e seu coeficiente de resistência do ar como 0,500 .A que altura um