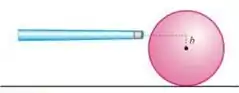
10.6P Calcule em termos do raio da bola, o parâmetro de impacto de uma tacada (Figura 10.11) para que a bola de sinuca tenha inicialmente movimento de rolamento.

Belezoca galera, vamos supor que a bola de sinuca tenha um raio , e além disso vamos dizer que a força que o taco faz sobre a esfera é , de forma que pela segunda lei de newton temos:

Onde á massa total da esfera, e é a aceleração resultante da tacada. Mas além disso essa força não é aplicada diretamente sobre o centro de massa, ela possui uma distância do centro, o que faz com que a força gere um torque resultante :

Só que a malandragem aqui é que o torque também pode ser escrito como o produto do momento de inércia pela aceleração angular :

E se a gente usar a relação entre aceleração angular e linear teremos que:

Igualando as expressões: