Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 9.Exercícios e Problemas - Ex. 7
9.7P Calcule o momento de inércia da régua fina mostrada na figura 9.17 em relação ao eixo .
Passo 1
Belejóia galerinha, a figura da nossa barra é dada por:
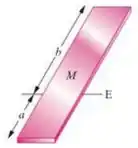
O momento de inércia de um objeto é dado por:
Nessa caso, podemos dividir nossa régua em duas, a parte e a parte , dessa maneira podemos calcular o momento de inércia de cada parte separadamente dado que:
Passo 2
Iradoso, pra descobrir as massas podemos lembrar que a densidade da régua é:
Logo temos que:
Já os raios, serão as distâncias de cada parte até o eixo , como estamos tratando de massas pontuais, temos que as distâncias serão:
Tal que o momento de inércia pode ser reescrito como:
Portanto, temos que:
E substituindo o valor de descobrimos que o momento de inércia final será:
Resposta
Exercícios de Livros Relacionados
Você é o gerente de projeto de uma empresa de manufatura. Uma das peças de máquina na linha de montagem é uma vareta fina e uniforme com 60,0 cm de extensão e massa de 0,400 kg. (a) Qual é o momento d
Uma esfera com raio R 0,200 m tem densidade r que diminui com a distância r a partir do centro da esfera, de acordo com r 3,00 × 103 kg/m3 (9,00 × 103 kg/m4 )r. (a) Calcule a massa total da esfera. (b
Um disco uniforme possui raio R0 e massa M0. Seu momento de inércia para um eixo perpendicular ao plano do disco no centro do disco é 1 / 2M 0 R 0 2 . Você deverá dividir o momento de inércia do disco
Uma nova espécie de enguia foi descoberta, com a mesma massa, porém com um quarto do comprimento e o dobro do diâmetro da enguia americana. Qual é a relação entre seu momento de inércia em torno de se
Determine o momento de inércia de um cone maciço uniforme em relação a um eixo que passa através de seu centro (Figura P9.90). O cone possui massa M e altura h. O raio do círculo de sua base é igual a