Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.3 - Ex. 19

Um aro de 2,20 kg e 1,20 m de diâmetro está rolando da esquerda para a direita sem deslizar, sobre um piso horizontal a constantes 3,0 rad/s. a) Com que velocidade o seu centro está se

movendo? b) Qual é a energia cinética total do aro? c) Ache o vetor velocidade de cada um dos seguintes pontos, do ponto de vista de uma pessoa em repouso sobre o chão: i) o ponto mais

alto do aro; ii) o ponto mais baixo do aro; iii) um ponto do lado direito do aro, a meio caminho entre o topo e a base. d) Ache o vetor velocidade para cada um dos pontos no item (c), só que do ponto de vista de alguém que se move com a mesma velocidade do aro.

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um aro de e de diâmetro está rolando da esquerda para a direita sem deslizar, sobre um piso horizontal a constantes .

Queremos encontrar a) a velocidade com que o seu centro está se movendo, b) a energia cinética total do aro e c) o vetor velocidade de cada um dos seguintes pontos, do ponto de vista de uma pessoa em repouso sobre o chão:

O ponto mais alto do aro;
o ponto mais baixo do aro;
um ponto do lado direito do aro, a meio caminho entre o topo e a base.

Depois temos que refazer a letra c) adotando o ponto de vista de alguém que se move com a mesma velocidade do aro.

Bom... para isso a gente precisa de alguns conceitos que vamos mostrar no Passo 2.

Bora lá!! 😉

Passo 2

Desde que está rolando sem escorregar, a aceleração da massa está relacionada à tensão por:

Onde é a velocidade do centro de massa, é o raio e é a velocidade angular.

E a energia cinética é dada por:

Onde é a massa do aro e é o momento de inércia.

E as velocidades dos pontos na borda do aro são como descritas na Figura 10.13, capitulo 10, do livro:

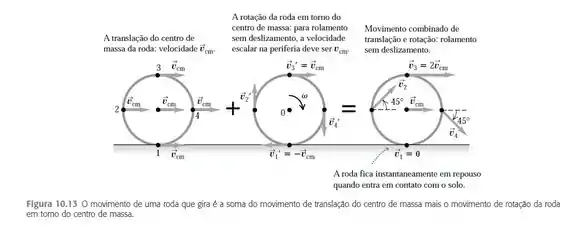
Temos os seguintes dados: e sabemos que para um aro girando em torno de um eixo no centro:

Agora bora aplicar!! 😉

Passo 3

Então, vamos calcular com que velocidade o seu centro está se movendo:

Passo 4

A energia cinética total do aro será dada por:

Passo 5

1. A velocidade no ponto mais alto é dada por:
2. No ponto mais baixo do aro:
3. Para encontrarmos a velocidade do ponto do lado direito do aro, a meio caminho entre o topo e a base fazemos:
Passo 6
Para alguém que se move para a direita em , o aro parece girar em torno de um eixo estacionário no centro.