Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Questões Conceituais - Ex. 8
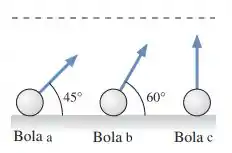
10.8. As três bolas da Figura Q10.8, todas de mesma massa, são arremessadas com a mesma rapidez segundo os ângulos mostrados. Ordene em sequencia decrescente, os módulos de suas velocidades ao atravessarem a linha horizontal. Explique. (Todas as três são arremessadas com velocidades suficientemente grande para que alcancem a linha.)
Passo 1
vamos supor que não tem nenhum atrito agindo sobre a bola, e que a linha horizontal está no ponto do eixo .
O caso da “Bola a” vai ser arremessada com um ângulo de em relação ao eixo positivo, com uma velocidade inicial a partir do solo, vai fazer um movimento oblíquo e em algum momento vai passar pela linha horizontal na altura . Vamos escrever esse movimento como uma equação de conservação de energia
A gente pode cortar a massa
Então
Passo 2
Agora vamos ver o caso da “Bola b”. Essa bola é lançada com a mesmas condições iniciais que a “Bola a”, mas agora o ângulo está em em relação ao solo. Vamos escrever a equação de conservação de energia
De novo podemos cortar a massa
E aí ficamos com
Olha só, a velocidade final da “Bola b” é igual a velocidade final da “Bola a”.
Passo 3
Agora só falta a “Bola c”. Essa bola é lançada diretamente para cima, com uma velocidade inicial e uma altura , exatamente igual as outras duas bolas. Vamos descrever esse movimento numa equação de conservação de energia.
Vamos, mais uma vez, cortar a massa
E aí ficamos com
Então todas as velocidades são iguais!!! Não faz sentido a gente ordenar as bolas, elas estarão todas na mesma posição.
Passo 4
Antes de ir para próxima questão, vamos discutir porque todas as velocidades são iguais.
Bom, a única força agindo na bola é a força gravitacional, e a força gravitacional, e a força gravitacional é uma força conservativa, isso quer dizer que o trabalho realizado por essa força não depende do caminho escolhido, só dos pontos inicial e final.
A força gravitacional só age na vertical, pelo menos na situação da bola que acabamos de estudar, sendo assim, o trabalho só depende dos pontos final e inicial no eixo , e todas as bolas tem esses pontos em comum, o ponto inicial é o solo e o ponto final é a linha horizontal, na altura , então o trabalho realizado em todas as bolas vai ser igual! Mas o que o trabalho tem a ver com a velocidade?
Aqui a gente tem que lembrar do teorema que diz que o trabalho é igual a variação da energia cinética. Todos os trabalhos são iguais, então, a variação da energia cinética de todas as bolas são iguais também. A energia cinética depende da massa e da velocidade. A massa e a velocidade inicial de todas as bolas são exatamente as mesmas, consequentemente, a velocidade final de todas as bolas tem que ser igual também.