Exercícios de Energia Cinética - Lista de Exercícios Resolvida
Questão 1
Você vence uma amiga, em uma corrida. No início, as duas tem a mesma energia cinética, mas ela está mais rápida do que você. Quando você eleva sua rapidez em por cento, vocês passam a ter a mesma rapidez. Se sua massa é , qual é a massa dela?
Ver solução completaQuestão 2
Dê um exemplo de uma partícula que tem energia cinética constante mas está acelerada. Pode uma partícula não acelerada ter energia cinética variável? Caso afirmativo, dê um exemplo.
Ver solução completaQuestão 3
Um pedaço de lixo espacial de tem uma rapidez de .
- Qual é a sua energia cinética?
- Qual passa a ser sua energia cinética, se sua rapidez é reduzida à metade?
- Qual passa a ser sua energia cinética, se sua rapidez é dobrada?
Questão 4
Um elétron com energia cinética igual a 1,22 x 103eV descola-se segundo um movimento circular em um plano perpendicular a um campo magnético uniforme. O raio da órbita é igual a 24,7cm. Calcule (a) a velocidade do elétron;
Ver solução completaQuestão 5
Um elétron com energia cinética igual a 1,22 x 103 eV desloca-se segundo um movimento circular em um plano perpendicular a um campo magnético uniforme. O raio da órbita é igual a 24,7cm. Calcule
(b) o campo magnético;
Ver solução completaQuestão 6
Duas lontras brincalhonas deslizam ao encontro uma da outra sobre uma superfície horizontal lamacenta (e, portanto, sem atrito). Uma delas, com massa de 7,50 kg, desliza para a esquerda a 5,00 m/s, enquanto a outra, com massa de 5,75 kg, escorrega para a direita a 6,00 m/s. Elas se agarram firmemente após colidirem.
(b) Quanta energia mecânica se dissipa durante essa brincadeira?
Ver solução completaQuestão 7
Uma bola de gude de 10,0 g desloca-se com velocidade de 0,400 m/s para a esquerda sobre uma pista horizontal sem atrito e colide frontalmente com outra bola de gude de 30,0 g que se desloca com velocidade de 0,200 m/s para a direita (Figura).
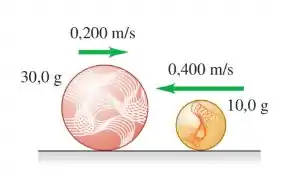
(c) Calcule a variação de energia cinética (isto é, a energia cinética depois da colisão menos a energia cinética antes da colisão) para cada bola. Compare os valores obtidos para cada bola.
Ver solução completaQuestão 8
Dois corpos cuja razão entre suas energias cinéticas é de e se movendo com igual momento possuem uma razão entre as massas de:
A.
B.
C.
D.
E. 2
Ver solução completaQuestão 9
Um bloco é lançado verticalmente para cima com uma velocidade inicial , atinge uma altura máxima e retorna ao ponto do lançamento, percorrendo uma distância total de .
a) Desprezando qualquer interação dissipativa entre o ar e o bloco, calcule em termos de e a aceleração da gravidade ;
b) Esboce um gráfico da energia potencial gravitacional e da energia cinética como função da distância percorrida entre e ;
c) Repita o item anterior de forma qualitativa, considerando agora que há uma interação dissipativa entre o ar e o bloco (nesse caso a altura máxima alcançada é menor que ). Inclua também no seu gráfico a energia térmica e energia de fonte do sistema Terra + bloco + ar.
Ver solução completaQuestão 10
Suponha que moles de um gás ideal diatômico sofre um processo termodinâmico de um estado inicial de pressão , volume e temperatura para um estado final de pressão , volume e temperatura . Ao longo deste processo termodinâmico, a pressão varia proporcionalmente ao volume. Além disso, a velocidade média quadrática das moléculas dobra de valor entre os estudos inicial e final. Nestas condições, calcule.
- (0,5) A temperatura final , expressando seu resultado em termos de . Dado: A energia cinética de translação média das moléculas de um gás ideal e , onde é a constante de Boltzmann.
- (i) A pressão final , expressando seu resultado em termos de e (ii) o volume final expressando seu resultado em termos de .
- O trabalho realizado pelo gás entre os estados inicial e final. Expresse seu resultado em termos de e .
- O calor requerido para levar o sistema do estado inicial ao final. Expresse seu resultado em termos de e . Dado: Um gás ideal diatômico tem calor específico molar , onde é a constante universal dos gases.
Questão 11
Dois barcos projetados para deslizar no gelo estão inicialmente em repouso sobre um lago congelado (que pode ser considerado uma superfície lisa sem atrito). Os barcos pretendem apostar uma corrida até um ponto que se encontra a uma distância de onde eles estão inicialmente. As velas dos barcos são idênticas de maneira que o vento exerce sobre os barcos a mesma força de módulo . Um dos barcos possui massa total e o outro (já consideradas as massas do tripulante de cada barco). Qual dos barcos cruza a linha de chegada primeiro? Qual possui maior energia cinética ao cruzar a linha de chegada?
a) Os barcos chegam ao mesmo tempo e cruzam a linha de chegada com mesma energia cinética.
b) O barco de massa chega primeiro mas o de massa chega com maior energia cinética.
c) Os barcos chegam ao mesmo tempo mas o de massa chega com maior energia cinética.
d) O barco de massa chega primeiro e cruza a linha de chegada com maior energia cinética.
e) Os barcos chegam ao mesmo tempo mas o de massa chega com maior energia cinética.
f) O barco de massa chega primeiro mas os dois barcos cruzam a linha de chegada com a mesma energia cinética.
Ver solução completaQuestão 12
Uma partícula movendo-se num plano pode ter uma das seguintes velocidades em metros por segundo: (a); (b); (c) ; (d) ; (e) fazendo com o eixo x. Ordene em ordem crescente as energias cinéticas da partícula.
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 13
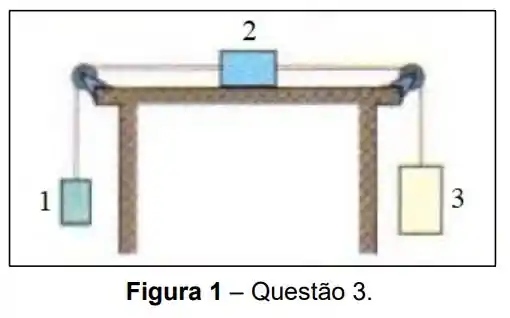
Na figura a seguir temos a imagem de três caixas, ligadas entre si por cordas, de massas desprezíveis, que passam por polias sem atrito. O bloco 2 está sobre uma superfície com coeficiente de atrito cinético de e as massas das caixas são , e . Ao liberarmos as caixas para se movimentarem, qual a tensão na corda da esquerda?
Questão 14
Em uma corrida, um pai tem metade da energia cinética do filho, que tem metade da massa do pai. Aumentando sua velocidade em , o pai passa a ter a mesma energia cinética do filho. Quais são as velocidade escalares iniciais do pai e do filho?
Ver solução completaQuestão 15
Um bloco de escorrega para baixo, a partir do repouso, em um plano inclinado que faz um ângulo de com a horizontal. O coeficiente de atrito cinético é de .
Neste mesmo instante, quanto vale a energia cinética do bloco?
Ver solução completaQuestão 16
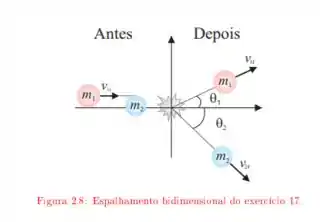
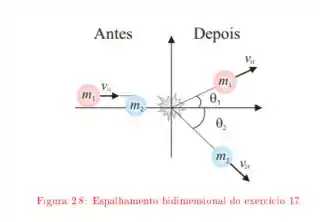
A corda da , e comprimento , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância da extremidade fixa a um pino no ponto é de . A bola, inicialmente em repouso, é liberada com o fio na posição horizontal, como mostra a figura, e percorre a trajetória indicada pelo arco tracejado. Qual é a velocidade da bola ao atingir o ponto mais baixo da trajetória e o ponto mais alto depois que a corda encosta no pino?
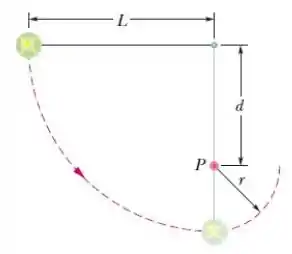
Questão 17
Um bloco de massa é deixado cair sobre uma mola vertical, inicialmente relaxada, de constante elástica . O bloco passa a ficar preso à mola, comprimindo-a até para momentaneamente. Nesta compressão: qual é o trabalho realizado pela força gravitacional que age sobre ele? qual é o trabalho realizado pela força da mola?; qual é a velocidade do bloco imediatamente antes dele atingir a mola?; se a velocidade no momento do impacto com a mola for duplicada, qual será a compressão máxima desta?
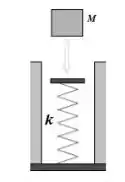
Questão 18
Um satélite desloca-se em uma órbita elíptica em torno da Terra. A distância do satélite ao centro da Terra é quatro vezes maior no apogeu do que no perigeu. O satélite tem velocidade e energia total no apogeu e, correspondentemente, e no perigeu. Encontre as razões:
Questão 19
“Minha jangada vai sair pro mar
Vou trabalhar meu bem querer
Se Deus quiser quando eu voltar do mar
Um peixe bom eu vou trazer
Meus companheiros também vão voltar
E a Deus do céu vamos agradecer.”
“Canção da Partida” de Dorival Caymmi.
Esta é a sublime e simples canção de Dorival Caymmi e expressa o desejo que todo pescador tem de ir e voltar da pesca.
Vamos supor que, ao ir para o mar a velocidade da jangada era de (pois estava contra a correnteza) e que sua massa era de e ao voltar, a velocidade da jangada era de (pois está a favor da correnteza) e com uma massa de (pois trouxeram peixes). A variação da energia cinética é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 20
Um móvel de massa , registra uma velocidade de . Qual a energia cinética deste móvel?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 21
O momento de inércia, possui propriedades similares às do centro de massa, pois ambos são dados na forma de uma integral. Sendo assim, no cálculo do momento de inércia é possível dividir o domínio de integração em subdomínios e posteriormente somar o resultado. Por exemplo, para a figura abaixo (um urso”), basta calcular o momento de inércia de cada uma das sub-regiões numeradas de a em relação ao eixo , e depois somar o resultado:
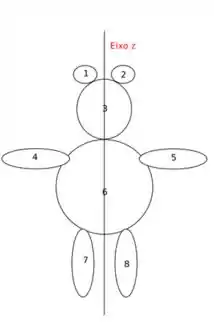
Sabendo disto, calcule o momento de inércia da figura abaixo em relação aos eixos e , supondo que as barras delgadas possuem massa desprezível e que as barras grossas possuem massa , são homogêneas e possuem secção reta circular de raio .
Dados: momento de inércia de um cilindro homogêneo de massa em relação ao eixo que passa pelo centro de sua secção reta de raio e pelo seu centro de massa: momento de inércia de uma barra homogênea de massa e comprimento em relação ao eixo que é perpendicular à extensão da barra e passa pelo seu centro de massa:
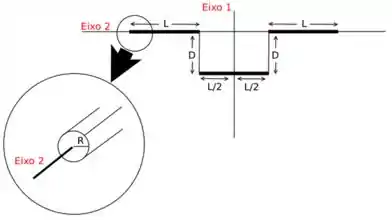
Questão 22
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
a) Qual deve ser o módulo da velocidade da bolinha no ponto mais baixo?
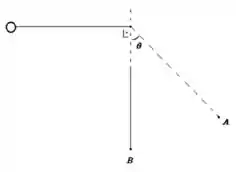
Questão 23
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
b) O módulo da força que o fio faz na bolinha no ponto mais baixo?
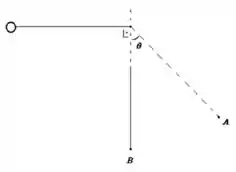
Questão 24
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
c) O módulo da velocidade da bolinha no ponto .
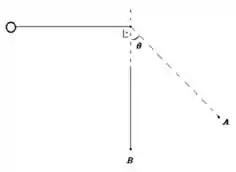
Questão 25
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
e) Qual deveria ser o módulo da velocidade mínima da bolinha no ponto inicial para que a bolinha desse a volta completa?
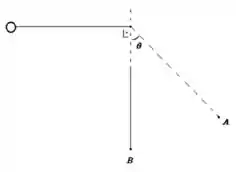
Questão 26
12. Uma bolinha de massa amarrada a um fio de comprimento é largada na posição vista na figura abaixo. Calcule:
d) O módulo da força que o fio faz na bolinha no ponto .
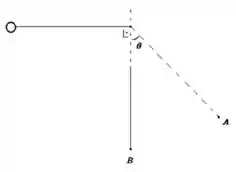
Questão 27
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
b) Se a energia mecânica total for determine as regiões permitidas para o movimento da partícula;
Ver solução completaQuestão 28
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
e) Se a partícula tem energia cinética nula quando posicionada em , qual é a energia mínima que deve ser fornecida para que ela possa atingir a posição ? Neste caso, qual sua energia cinética em ?
Ver solução completaQuestão 29
Uma partícula está submetida a uma força dada pela energia potencial .
b) Qual é a variação de energia cinética entre os pontos e ? Este resultado depende do caminho percorrido pela partícula? Justifique.
Ver solução completaQuestão 30
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
a) Quais são os pontos ou as regiões de equilíbrio?
Ver solução completaQuestão 31
Uma partícula de massa move-se ao longo do eixo sob a ação de uma força conservativa em uma região onde a energia potencial varia conforme o gráfico apresentado na figura .
c) Determine a energia cinética da partícula em ;
Ver solução completaQuestão 32
“Minha jangada vai sair pro mar
Vou trabalhar meu bem querer
Se Deus quiser quando eu voltar do mar
Um peixe bom eu vou trazer
Meus companheiros também vão voltar
E a Deus do céu vamos agradecer.”
“Canção da Partida” de Dorival Caymmi.
Esta é a sublime e simples canção de Dorival Caymmi e expressa o desejo que todo pescador tem de ir e voltar da pesca.
Vamos supor que, ao ir para o mar a velocidade da jangada era de (pois estava contra a correnteza) e que sua massa era de e ao voltar, a velocidade da jangada era de (pois está a favor da correnteza) e com uma massa de (pois trouxeram peixes). A variação da energia cinética é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 33
Qual a energia cinética de uma partícula de massa cuja velocidade vale ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 34
(Cap 7 – Ex 3) Um próton (massa ) está sendo acelerado em linha reta a em um acelerador de partículas. Se o próton tem uma velocidade inicial de e se desloca , determine (a) a velocidade e (b) o aumento da energia cinética do próton.
Ver solução completaQuestão 35
(Cap 7 – Ex 2) Se um foguete Saturno V e uma espaçonave Apolo acoplada ao foguete tinham uma massa total de , qual era a energia cinética quando atingiram uma velocidade de ?
Ver solução completaQuestão 36
(Cap 7 – Ex 5) Em uma corrida, um pai tem metade da energia cinética do filho, que tem metade da massa do pai. Aumentando a velocidade em , o pai passa a ter a mesma energia cinética do filho. Qual é a velocidade escalar inicial (a) do pai e (b) do filho?
Ver solução completaQuestão 37
(Cap 7 – Ex 6) Uma conta com uma massa de está se movendo no sentido positivo do eixo . A partir do instante , no qual a conta está passando pela posição com uma velocidade de , uma força constante passa a agir sobre a conta. A Fig. 7-22 mostra a posição da conta nos instantes , , e . A conta para momentaneamente em . Qual é a energia cinética da conta em ?

Questão 38
Numa colisão perfeitamente elástica entre dois corpos rígidos:
(A) O momentum (momento linear) de cada objeto se conserva.
(B) A energia cinética de cada objeto se conserva.
(C) O momentum (momento linear) do sistema (corpo 1+corpo 2) se conserva e a energia cinética do sistema não se conserva.
(D) Tanto a energia cinética quanto o momentum (momento linear) do sistema se conservam.
(E) A energia cinética do sistema se conserva, mas o momentum (momento linear) do sistema não se conserva.
Ver solução completaQuestão 39
Dois objetos, com massas e , têm a mesma energia cinética e ambos estão se movendo para a direita. A mesma força constante é aplicada para a esquerda sobre as duas massas. Se , a razão entre a distância percorrida por até parar e a percorrida por até parar é:
(a) .
(b)
(c) .
(d) .
(e) .
Ver solução completaQuestão 40
O cabo de um elevador de rompe-se, quando ele está parado no primeiro andar. No instante do rompimento, o piso do elevador encontra-se a uma distância acima de uma mola amortecedora, cuja constante de mola é . Um sistema de segurança prende os trilhos laterais que servem de guia, de modo que uma força de atrito constante de opõe-se ao movimento do elevador após o rompimento do cabo. Determine:
A velocidade de elevador imediatamente antes de atingir a mola;
Ver solução completaQuestão 42
Uma partícula de massa move-se apenas sob a ação de uma força conservativa , onde é medido em metros e em Newtons. A variação da energia cinética da partícula quando ela se move da posição para a posição é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 43
Um anel de espessura desprezível rola sem deslizar sobre uma superfície horizontal. A razão entre as energias cinéticas de rotação e translação do anel é igual a
Questão 45
Uma massa de tem uma certa velocidade . Sua energia cinética será:
A.
B.
C.
D.
E.
Ver solução completaQuestão 46
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
calcule a energia cinética do cilindro quando .
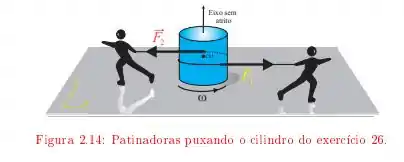
Questão 47
34. Uma mesa de coquetel tem um tampo giratório, que é uma tábua circular de raio e massa , capaz de girar com atrito desprezível em torno de um eixo vertical da mesa. Uma bala de massa e velocidade , disparada por um convidado, numa direção horizontal, vai encravar-se na periferia da tábua.
(b) Que fração da energia cinética inicial é perdida no impacto?
Ver solução completaQuestão 48
Uma bala de é disparada com velocidade de sobre um pêndulo balístico com massa igual a , suspenso por uma corda de comprimento igual a . Calcule (a) a altura vertical atingida pelo pêndulo; (b) a energia cinética inicial da bala; (c) a energia cinética da bala e do pêndulo imediatamente depois de a bala ficar retida no pêndulo.
Ver solução completaQuestão 49
Dois patinadores, cada um de massa , deslizando sobre uma pista de gelo, com atrito desprezível, aproximam-se com velocidades iguais e opostas de módulo , segundo retas paralelas, as quais estão separadas por uma distância .
Calcule a energia cinética do sistema antes e depois dos patinadores se unirem. Explique o resultado.
Ver solução completaQuestão 50
42. Uma bola de bilhar de raio e massa , inicialmente em repouso, recebe uma tacada seca. O impulso do taco é horizontal e aplicado à distância abaixo da linha horizontal do centro. A velocidade linear da bola é .
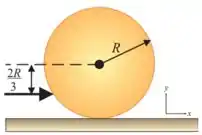
(c) Qual a energia cinética inicial da bola? Assuma e .
Ver solução completaQuestão 51
A figura mostra três forças aplicadas a um baú que se desloca três metros para a esquerda sobre um piso sem atrito. Os módulos das forças são: , e ; o ângulo indicado é . Nesse deslocamento, (b) A energia cinética do baú aumenta ou diminui? Justifique.
Ver solução completaQuestão 52
Uma bala de é disparada com velocidade de sobre um pêndulo balístico com massa igual a , suspenso por uma corda de de comprimento. Calcule
c) a energia cinética da bala e do pêndulo imediatamente depois de a bala ficar retida na madeira do pêndulo.
Ver solução completaQuestão 53
Uma bala de é disparada com velocidade de sobre um pêndulo balístico com massa igual a , suspenso por uma corda de de comprimento. Calcule
b) a energia cinética inicial da bala.
Ver solução completaQuestão 54
Sobre uma mesa de ar horizontal sem atrito, o disco de hóquei A (com massa igual a ) se desloca ao encontro do disco B (com massa igual a ), que inicialmente está em repouso. Depois da colisão, o disco A possui velocidade igual a para a esquerda e o disco B possui velocidade igual a para a direita.
(b) Calcule a variação da energia cinética total do sistema ocorrida durante a colisão.
Ver solução completaQuestão 55
Quais das afirmações a seguir são verdadeiras sobre a energia cinética? Inclua todos que se aplicam.
- A energia cinética é a forma de energia mecânica que depende da posição de um objeto.
- Se um objeto estiver no solo, ele não terá energia cinética.
- Objetos com movimentos mais rápidos sempre tem uma energia cinética maior
- A energia cinética é uma grandeza escalar
- Um objeto tem uma energia cinética de . Se sua velocidade fosse o dobro, então sua energia cinética seria de .
- Um objeto nunca pode ter uma energia cinética negativa.
- Um objeto de é acelerado do repouso a uma velocidade de . Este objeto ganha de energia cinética.
Escolha uma:
- 4-7
- Nenhuma das outras alternativas ou, duas ou mais alternativas.
- 2-3-5-6
- 4-5-6
- 3-4-5-6
- 4-6
- 3-6
- 2-3-4-5-6
- 3-4-7
Questão 56
Uma nave espacial se move em volta da terra com velocidade constante, numa órbita circular de raio . Acionando os foguetes da nave numa determinada sequência, o piloto manobra a nave de maneira a transferi-la para uma nova órbita circular, no mesmo plano, mas de raio . Em relação às variações de energia cinética e potencial gravitacional da nave na transferência entre as duas órbitas, qual afirmação é correta?
- A energia cinética diminui e a energia potencial aumenta.
- A energia cinética aumenta e a energia potencial diminui.
- A energia cinética não se altera e a energia potencial aumenta.
- A energia cinética não se altera e a energia potencial diminui.
- As energias cinética e potencial aumentam.
Questão 57
Um carro de se move com uma velocidade de módulo . Se um caminhão de possui uma energia cinética vezes maior que a do carro em questão, qual o módulo da velocidade do caminhão?
(A) 63 km/h
(B) 45 km/h
(C) 54 km/h
(D) 36 km/h
(E) 90 km/h
Ver solução completaQuestão 58
Um projétil de é disparado com uma velocidade inicial com componentes e a partir de um ponto sobre a superfície da Terra. A resistência do ar é desprezível. Qual é a energia cinética do projétil quando ele alcança o ponto mais alto da sua trajetória?
(a) zero
(b)
(c)
(d)
(e)
Ver solução completaQuestão 59
A figura (a) mostra duas forças horizontais que agem sobre um bloco que no instante está deslizando para a direita sobre uma superfície sem atrito. A figura (b) mostra três gráficos da energia cinética deste bloco em função do tempo . Qual dos gráficos corresponde melhor a cada uma das três seguintes situações: 1) ; 2) ; 3) ?
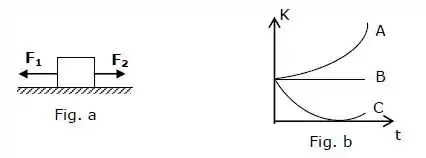
(A) A, B, C
(B) A, C, B
(C) C, B, A
(D) B, A, C
(E) B, C, A
Ver solução completaQuestão 60
Uma caixa de massa igual a desliza por um plano com inclinação de A aceleração da caixa é de e o plano inclinado tem de comprimento.
(a) Qual é a energia cinética da caixa quando ela atinge a base do plano inclinado?
(b) Quanto trabalho é gasto para superar o atrito?
(c) Qual é a magnitude da força de atrito que atua na caixa conforme ela desliza pelo plano inclinado?
Ver solução completaQuestão 61
Um elétron com energia cinética igual a 1,22 x 103 eV descola-se segundo um movimento circular em um
plano perpendicular a um campo magnético uniforme. O raio da órbita é igual a 24,7cm. Calcule (c) o tempo que o elétron gasta para dar uma volta completa
(período).
Ver solução completa