Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 9.Problemas Adicionais - Ex. 125

125- Um núcleo atômico em repouso na origem de um sistema de coordenadas x y se desintegra em três partículas. A partícula 1, com massa de 16.7 × 10 - 27   k g , se afasta da origem com uma velocidade ( 6.00 × 10 6   m / s ) i ^ ; a partícula 2, com uma massa de 8.35 × 10 - 27   k g , se afasta da origem com uma velocidade - 8.00 × 10 6   m / s j ^ .

(a) Na notação dos vetores unitários, qual é o momento linear da terceira partícula, cuja massa é 11,7 × 10 −27 kg?

(b) Qual é a energia cinética produzida pela desintegração?

Passo 1

  1. A terceira partícula tem velocidade igual a v 3

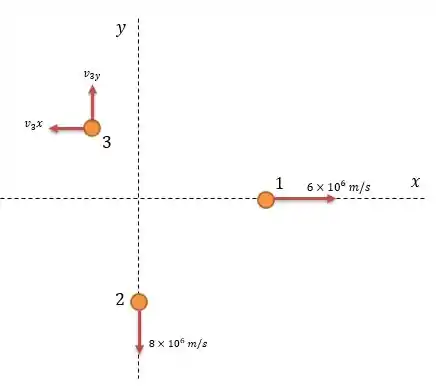
    2. Como o núcleo estava parado logo a conservação dos momentos lineares será :

    0 = m 1 v 1 + m 2 v 2 + m 3 v 3

    Então o momento linear na partícula 3 igual a m 3 v 3 será:

    p 3 = m 3 v 3 = - m 1 v 1 - m 2 v 2

    p 3 = - 16.7 × 10 - 27 × 6 × 10 6 i ^ - 8.35 × 10 - 27 × - 8 × 10 6 j ^

    p 3 = - 1 × 10 - 19 i ^ + 6.68 × 10 - 20 j ^   k g   m s

    Passo 2

  2. A energia cinética total é a somatória da energia cinética de todas as partículas, ou seja:

E c = 1 2 m 1 v 1 2 + 1 2 m 2 v 2 2 + 1 2 m 3 v 3 2

Porém precisamos encontrar o módulo da velocidade da partícula 3. Para isso vamos fazer:

p 3 = m 3 v 3 = - 1 × 10 - 19 i ^ + 6.68 × 10 - 20 j ^

Como a massa dessa partícula é de m 3 = 11.7 × 10 - 27   k g , logo a velocidade será:

v 3 = - 10 - 19 11.7 × 10 - 27 i ^ + 6.68 × 10 - 20 11.7 × 10 - 27 j ^

v 3 = - 8.55 × 10 6 i ^ + 5.71 × 10 6   j ^

O módulo da velocidade da partícula 3 será:

v 3 = 8.55 × 10 6 2 + 5.71 × 10 6 2 = 10.28 × 10 6   m / s

Passo 2

Calculando finalmente a energia cinética da partícula temos:

E c = 1 2 × 16.7 × 10 - 27 × 6 × 10 6   2 + 1 2 8.35 × 10 - 27 × - 8.00 × 10 6 2

+ 1 2 11.7 × 10 - 27   × 10.28 × 10 6 2

Isso tudo nos dá:

E c = 1.19 × 10 - 12   J

Resposta

a )   - 1 × 10 - 19 i ^ + 6.68 × 10 - 20 j ^   k g   m s

b ) 1.19 × 10 - 12   J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(c) Depois de passar pelo silo, ocorre um vazamento, e os grãos começam a vazar verticalmente por um furo no piso do vagão, a uma taxa constante. O vagão deve aumentar sua rapidez enquanto perde massa
(b) Se o vagão esta reduzindo sua velocidade, isto significa que existe alguma força externa atuando sobre ele.De onde vem essa força?
28. Um vagão ferroviário permanece rolando sobre os trilhos enquanto grãos de um silo estão caindo dentro dele a uma taxa constante.(a) A conservação da quantidade de movimento exige que o vagão deve
Um canhão montado sobre uma carreta, apontado numa direção que forma um ângulo de 30 ° com a horizontal, atira uma bala de 50K g , cuja velocidade na boca do canhão é de 300m / s . A massa total do ca
Um atirador, com um rifle de 2 Kg apoiado ao ombro, dispara uma bala de 15g, cuja velocidade na boca da arma( extremidade do cano) é de 800 m/s. a) Com que velocidade inicial a arma recua? b) Que impu