12.8. Uma massa pontual de 8,0 kg e outra massa pontual de 15,0 kg são mantidas fixas a 50,0 cm de distância. Uma partícula de massa m é solta de um ponto entre as duas massas a 20,0 cm da massa de 8,0 kg ao longo da linha que conecta as duas massas fixas. Ache o módulo, a direção e o sentido da aceleração da partícula.
Passo 1
Vamos começar fazendo um desenho do que está acontecendo
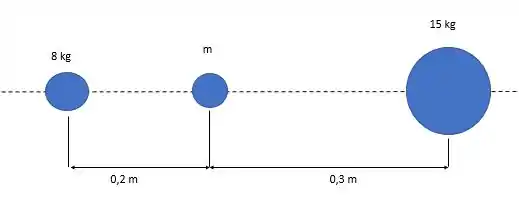
Bem, as bolas se atraem uma à outra, logo a linha de ação da força está na mesma direção que a linha tracejada na figura, ela cruza todos os centros gravitacionais das bolas.
Vamos lembrar de como se calcular a força de atração gravitacional
Onde e são as massas, é a distância entre os centros de gravidade dos corpos e é a constante gravitacional universal
Passo 2
Agora que já sabemos a direção da força, temos que calcular o módulo e o sentido. Bom para começar a calcular vamos definir que o sentido positivo é para à direita.
A gente quer saber somente das forças exercidas na partícula, então a força que vamos calcular é a força de interação entre a esfera da esquerda e a partícula somado com a força de interação entre partícula e a esfera da direita.
Agora é só calcular o módulo
Mas como a gente tinha adotado a direita como sentido positivo, e o módulo resultante deu negativo, então significa que o sentido é para a esquerda. Então
Módulo:
Direção: A linha tracejada da figura
Sentido: Para esquerda
Passo 3
Repare que o que fizemos ainda não é a resposta, nós achamos a direção, módulo e sentido da força, mas o exercício pede da aceleração, bom sabemos pela segunda lei de Newton que
Ou seja o vetor Força é igual ao vetor aceleração multiplicado por um escalar, ou seja, o sentido e direção da aceleração são os mesmos da Força. Agora só falta calcular o módulo.
Podemos de novo usar a segunda lei de Newton
Por tanto
Então
Módulo:
Direção: A linha tracejada da figura
Sentido: Para esquerda
Resposta
Módulo:
Direção: A linha que cruza os centros gravitacionais das esferas
Sentido: Para esquerda