Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 13.Exercício - Ex. 4
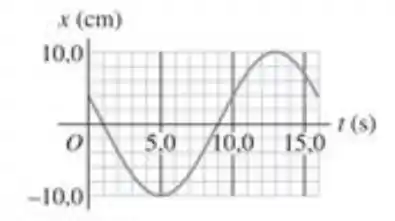
13.4. O deslocamento de um objeto oscilando em função do tempo é mostrado na Figura 13.30. Quais são (a) a frequência; (b) a amplitude; (c) o período; (d) a frequência angular desse movimento?
Passo 1
Vamos calcular a frequência. Bom pelo gráfico podemos ver que o objeto completou uma oscilação em 16 segundos. Então 16 segundos é o período, e como, por definição, a frequência é o inverso do período
Passo 2
Agora vamos para o item (b). Bom, a amplitude é a maior distância a partir do ponto de equilíbrio que há numa oscilação, então são os extremos do gráfico. Logo a amplitude é
Passo 3
É a vez do item (c), o período. Mas... Esse a gente já calculou no passo 1 😊. Então a gente pode ir para o item (d), calcular a frequência angular, que por definição é
Então
Resposta
Exercícios de Livros Relacionados
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen [ 4,00m - 1 x - 7,00s - 1 t ] .
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 2,00m m 20m - 1 x - 4,0s - 1 t 0,5 .
Quando o som sai do ar e penetra na água, sua frequência se altera? E sua velocidade? E seu comprimento de onda? Explique seu raciocínio.
O herói de um filme de aventura escuta a aproximação de um trem colocando seu ouvido no trilho. Por que esse método funciona melhor para perceber a aproximação do trem do que simplesmente escutar pelo
(a) Um nível sonoro de O dB significa que não há som? (b) Existe algum significado físico para um som ter um nível de intensidade negativo? Se houver, qual? (c) Uma intensidade sonora nula significa q