Exercícios de Introdução a Ondas - Lista de Exercícios Resolvida
Questão 1
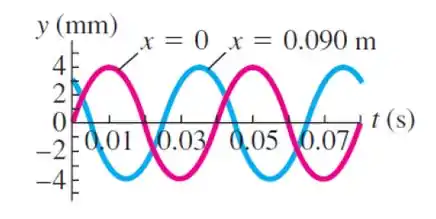
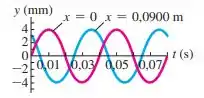
Uma onda senoidal se propaga ao longo de uma corda sob tensão. A figura 1 fornece a inclinação da corda ao longo do eixo no instante . Suponha que a equação da onda progressiva é do tipo
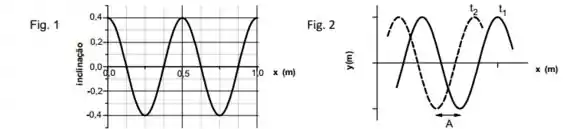
- Calcule a amplitude da onda progressiva.
- Calcule a constante de fase.
- Calcule a frequência da onda progressiva.
- Escreva a equação , com os valores pra , e , e com o sinal correto em frente a , baseando-se na análise das figuras 1 e 2.
A figura 2 mostra dois instantes diferentes de um pedaço da mesma onda progressiva da figura 1. Na figura , e
Questão 2
O deslocamento de uma onda que se propaga no sentido negativo do eixo é , onde está em , e em . Quais são:
A frequência.
O comprimento de onda.
A velocidade da onda.
Ver solução completaQuestão 3
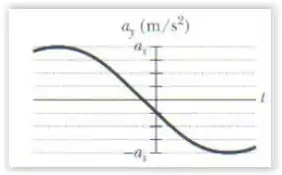
A figura abaixo mostra a aceleração transversal em função do tempo do ponto de uma corda, quando uma onda com a forma geral passa pelo ponto. A escala do eixo vertical é definida por . Qual é o valor de ?
Questão 4
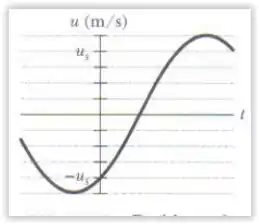
A figura abaixo mostra a velocidade transversal em função do tempo para o ponto de uma corda situado em , quando uma onda passa por ele. A escala do eixo vertical é definida por . A onda tem a forma . Qual é o valor de ?
Questão 5
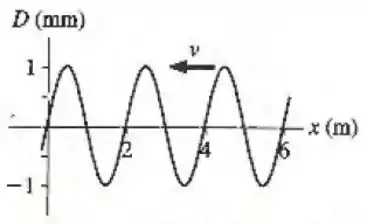
Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A velocidade da onda é de . Assuma que a onda é da forma .
Determine a amplitude e o comprimento de onda.
Encontre o período e o sinal que precede .
Determine a velocidade transversal máxima de uma partícula da corda.
Determine a constante de fase .
Ver solução completaQuestão 6
Uma onda possui frequência angular de rad/s e um comprimento de onda de m. Calcule:
- O número de onda;
- A velocidade de onda.
Questão 7
A função de onda para uma onda progressiva em uma corda esticada é (em unidades do SI):
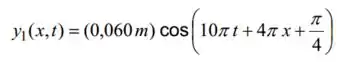
Suponha que a corda possui uma massa por unidade de comprimento de
- Obtenha o comprimento de onda, a velocidade e o sentido de propagação da onda.
- Obtenha o valor máximo de velocidade transversal da corda. Para a posição , em que instantes esse valor máximo ocorre? (Dê os dois primeiros, para
Questão 8
- Escreva, literalmente, a expressão de uma onda harmônica progressiva unidimensional, propagando-se no sentido positivo do eixo x, em termos da amplitude , da frequência e do comprimento de onda .
- A partir dessa expressão, determine a velocidade máxima com que um elemento do meio se movimenta.
Ver solução completaQuestão 9
A figura é um gráfico-instantâneo, para , de uma onda de que se propaga para a esquerda.
Qual é a velocidade da onda?
Qual é sua constante de fase?
Escreva a equação para os deslocamentos produzidos no meio por esta onda.
Ver solução completaQuestão 10
Uma onda senoidal se propaga em uma corda. O tempo necessário para que um certo ponto da corda se mova do deslocamento máximo até zero é . Quais são:
- O período;
- A frequência da corda.
- O comprimento de onda é , qual é a velocidade da onda?
Questão 11
Uma onda senoidal se desloca numa corda com velocidade 3,7 m/s no sentido negativo do eixo x.
As cristas da onda passam cinco vezes por segundo pelo ponto x = 0. No instante t = 0, esse ponto da corda está deslocado para cima de 0,5m com respeito à sua posição de equilíbrio. Este valor corresponde à metade do deslocamento que é atingido quando a crista passa por lá.
Baseado nessas informações, qual é a expressão matemática que descreve esta onda?
a)
b)
c)
d)
e)
Ver solução completaQuestão 12
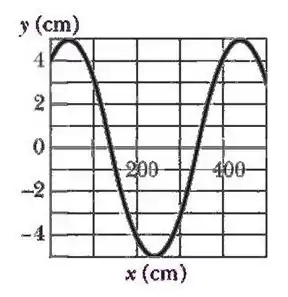
Uma onda senoidal se propaga ao longo de uma corda sob tensão. A figura 1 fornece a inclinação da corda ao longo do eixo no instante . Suponha que a equação da onda progressiva é do tipo
- Calcule a amplitude da onda progressiva.
- Calcule a constante de fase.
- Calcule a frequência da onda progressiva.
- Escreva a equação , com os valores pra , e , e com o sinal correto em frente a , baseando-se na análise das figuras 1 e 2.
A figura dois mostra dois instantes diferentes de um pedaço da mesma onda progressiva da figura 1. Na figura , e
Questão 13
Uma onda senoidal transversal com está se propagando no sentido de crescente. O deslocamento da partícula em , a partir do equilíbrio e em função do tempo, é mostrado na figura.
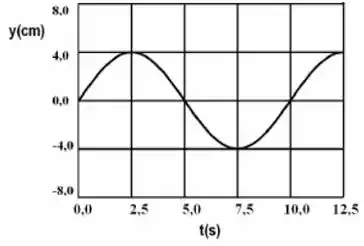
- Faça um esboço da onda no instante no trecho contido entre os pontos e . Indique claramente a amplitude, o comprimento de onda e o sinal da derivada em .
- Qual a velocidade de propagação da onda?
- Escreva a função que descreve a onda em qualquer e .
- Calcule a velocidade transversal da partícula em e
Questão 14
Uma corda de violino de comprimento de vibra no seu modo fundamental com uma frequência de . Sabendo que a velocidade do som no ar é , qual é o comprimento da onda que irá alcançar os seus ouvidos?
Questão 15
Uma onda plana harmônica de comprimento , amplitude e freqüência propaga-se numa superfície líquida. No instante observa-se uma partícula, que bóia nesta superfície, na coordenada vertical . Qual será sua coordenada em ?
Questão 16
As curvas A e B representam duas fotografias sucessivas de uma corda na qual se propaga um pulso. O intervalo de tempo entre as fotografias é menor que o período da onda e vale 0,10s.
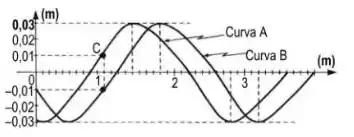
Podemos afirmar que a velocidade de propagação da onda na corda e a velocidade média do ponto C da corda, nesse intervalo de tempo, valem, respectivamente quanto?
Ver solução completaQuestão 17
Um satélite exploratório do planeta Júpiter transmite dados para a Terra por uma onda de rádio com frequência de 200 MHz. Qual é o comprimento de onda desta onda de rádio e quanto tempo aproximadamente o sinal demora para percorrer os 800 milhões de quilômetros que separam Júpiter e Terra?
- 2,0 m; 20 min
- 1,0 m; 15 min
- 1,5 m; 30 min
- 1,5 m; 45 min
- 3,0 m; 20 min.
Dado:
Ver solução completaQuestão 18
Duas canoas estão em um lago separadas por 10 m de distância. Uma onda na água passa continuamente pelas duas canoas. Quando uma canoa está no ponto mais alto da onda, a outra está no ponto mais baixo. Cada canoa sobe e desce (ou desce e sobe) em um intervalo de 8,0 s. Com relação à onda, não existe nenhuma crista ou vale entre as
duas canoas. Determine a velocidade da onda.
Questão 19
A figura mostra o deslocamento de uma dada posição do meio enquanto uma onda senoidal se desloca e o deslocamento da mesma onda num determinado instante, como uma função da posição. Qual é a velocidade da onda?
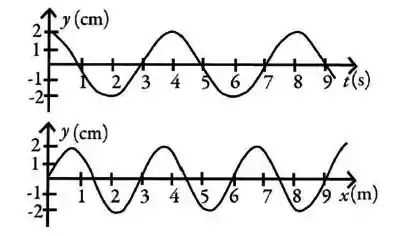
- 0.38 m/s
- 0.75m/s
- 1.5m/s
- 3.0m/s
- 12.0m/s
Questão 20
O perfil de onda transversal progressiva em uma corda muito longa é dado, em unidades do sistema internacional por:
Sabendo que a tensão aplicada na corda é de , determine:
- A amplitude de vibração da corda.
- O comprimento de onda e a frequência (Hz).
- O sentido e a velocidade de propagação da onda.
- A distância, ao longo da corda, de dois pontos cuja defasagem é
Questão 21
Em uma corda é observada uma onda cuja função de onda é dada por:
onde e estão em centímetros e t em segundos. Determine:
- O comprimento de onda e a frequência das duas ondas progressivas que formam a onda acima;
- A velocidade de propagação das ondas na corda;
- As funções de onda, ) e das duas ondas que geram a onda acima;
- A posição dos nós na corda;
- Mostre que a onda obedece à equação de onda.
- Sabendo que a corda está vibrando no quarto harmônico, com extremidades fixas, represente graficamente a onda e determine o comprimento da corda.
Questão 22
O gráfico-historia de uma onda senoidal que se desloca na direção positiva do eixo a , e mostrado na figura abaixo. A equação de deslocamento dessa onda é:
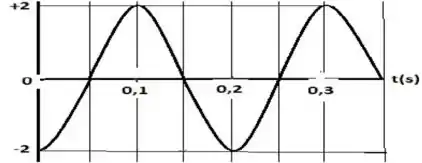
Questão 23
Um menino em passeio de final de semana visita o lago do Quitandinha, na cidade de Petrópolis, no Rio de Janeiro. Ao jogar no lago comida para os peixes, provoca ondas de 2,0 cm de comprimento de onda, com velocidade de 3,0 cm/s. Considerando estas informações, determine a frequência destas ondas.
- 9 Hz
- 18 Hz
- 12 Hz
- 5 Hz
- 1,5 Hz
Questão 24
Uma menina executa um movimento vibratório em uma corda presa a parede a cada . Sabendo que a corda tensionada possui de comprimento e que uma crista produzida leva para chegar a parede, determine o comprimento de onda produzido.
- 5m
- 40m
- 0,4m
- 2,5m
- 10m
Questão 25
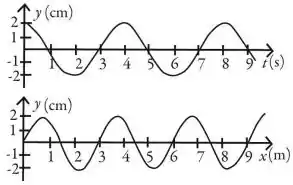
A figura mostra o gráfico-instantâneo ( em um tempo fixo) e o gráfico-história ( em uma dada posição fixa) de uma mesma onda. Qual a frequência desta onda?
A)
B)
C)
D)
E)
Ver solução completaQuestão 26
Encontre a velocidade de uma onda oceânica cujo deslocamento vertical em função do tempo t é dado por , onde todas as grandezas estão em unidades SI.
A)
B)
C)
D)
E)
Ver solução completaQuestão 27
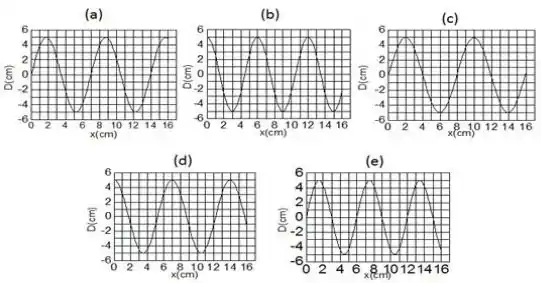
Uma onda se propaga em uma corda segundo a equação , com , e ω = . Qual dos gráficos abaixo melhor representa esta onda, no instante ?
Questão 28
Considere as seguintes afirmativas:
(I) Podemos afirmar que uma onda progressiva que se move ao longo de uma corda transfere energia ao longo de sua direção de propagação.
(II) Uma onda sonora não se propaga no vácuo, pois é acompanhada de um transporte de matéria de um ponto para outro do espaço.
(III) Não existe propagação de energia por meio de uma onda estacionária, pois a energia está aprisionada entre os nós.
(IV) A intensidade de uma onda não depende de sua amplitude.
(V) Uma onda sonora é uma onda de pressão.
Quais as afirmativas são verdadeiras?
- Apenas I
- Apenas II
- I e III
- I, III e V
- Nenhuma das alternativas
Questão 29
10. Duas ondas se propagam no mesmo sentido e com a mesma amplitude formando o padrão de batimento mostrado na figura abaixo. Considere , e .
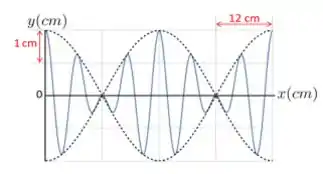
A velocidade de grupo, , vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 30
9. Duas ondas se propagam no mesmo sentido e com a mesma amplitude formando o padrão de batimento mostrado na figura abaixo. Considere , e .
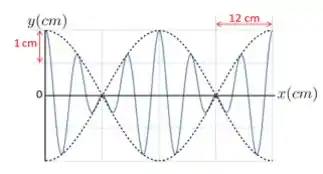
Os valores de e para as duas ondas podem ser escritos como:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 31
11. Duas ondas se propagam no mesmo sentido e com a mesma amplitude formando o padrão de batimento mostrado na figura abaixo. Considere , e .
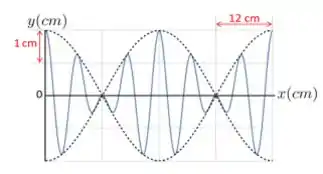
A velocidade de fase, , vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 32
A figura abaixo mostra uma onda transversal propagando numa corda tensionada com velocidade v no sentido de . Denotando por as velocidades tranversais dos pontos 1, 2, 3 e 4 da corda, podemos afirmar que:
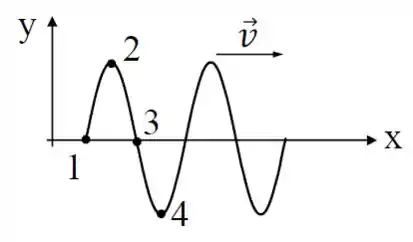
a)
b)
c)
d)
e)
Ver solução completaQuestão 33
a)Duas ondas sonoras, oriundas de fontes diferentes e de frequências iguais a , se propagam na mesma direção (eixo- ) e no mesmo sentido com velocidade de . Sabendo-se que as duas fontes emitem em fase, qual a diferença de fase entre as ondas num ponto que está a de uma fonte e a da outra fonte?
Ver solução completaQuestão 34
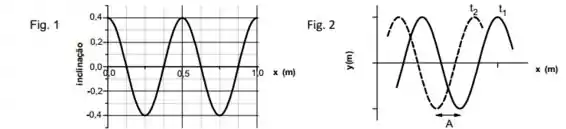
Considere que uma corda esticada está oscilando na direção vertical (y) por conta de uma onda harmônica que viaja ao longo da direção horizontal (x).
Os gráficos ao lado mostram a posição vertical de um certo elemento de corda em função do tempo (Gráfico 1) e o perfil da onda que está se propagando na corda, em um determinado instante de tempo, em função da posição horizontal (Gráfico 2). Sendo assim, quais são a velocidade da onda, , e a velocidade máxima de um certo elemento de corda, , em unidades de m/s ?
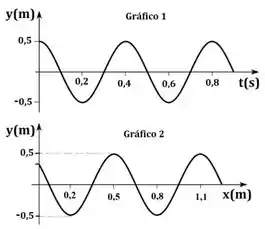
- ,
- ,
- ,
- ,
- ,
- ,
- ,
- ,
Questão 35
A função abaixo que descreve uma onda transversal se propagando no sentido negativo do eixo x com amplitude 0,003 m, frequência 5 Hz e velocidade 300 m/s é (para x e y em metros e t em segundos):
Questão 36
Uma onda progressiva propagando-se em uma corda é dada pela equação:
Com unidades dadas no SI. A velocidade da onda é:
a) 1,6 m/s;
b) 3,2 m/s;
c) 0,8 m/s;
d) 2,6 m/s;
e) 4,8 m/s;
Ver solução completaQuestão 37
Duas ondas senoidais idênticas, com períodos T, propagam-se no mesmo sentido. A segunda onda se origina no mesmo ponto que a primeira, mas depois de um certo intervalo de tempo. Sabendo que a amplitude da onda resultante é a mesma que a de cada uma das duas ondas individualmente, qual o intervalo mínimo de tempo possível entre os momentos de início das duas ondas?
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaQuestão 38
A figura mostra um instantâneo de três ondas que são produzidas separadamente em uma corda que está esticada ao longo do eixo x e submetida a uma certa tensão T. Quatro elementos da corda estão indicados pelas letras a, b, c e d. Se 1, 2, 3, representa o comprimento de onda da onda i, pode-se dizer que:
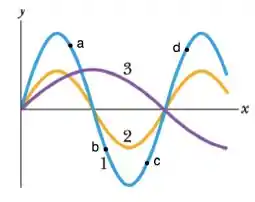
a) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.
b) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elemento c e d no sentido negativo.
c) . No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e b da corda estão se movendo no sentido positivo do eixo y e os elementos c e d no sentido negativo.
d) . No momento do instantâneo, se a onda 1 se propaga no sentido negativo do eixo x, os elementos a e d da corda estão se movendo no sentido positivo do eixo y e os elementos b e c no sentido positivo.
e) l. No momento do instantâneo, se a onda 1 se propaga no sentido positivo do eixo x, os elementos a e d da corda estão se movendo no sentido negativo do eixo y e os elementos b e c no sentido positivo.
Ver solução completaQuestão 39
Um dado ponto em uma corda por onde passa uma onda senoidal apresenta maior velocidade quando
A) o módulo da aceleração é máximo
B) o módulo do deslocamento é máximo
C) o módulo do deslocamento é mínimo
D) o módulo do deslocamento é metade da amplitude
E) o módulo do deslocamento é um quarto da amplitude
Ver solução completaQuestão 40
A equação de uma onda é: , onde x e y estão em metros e t está em segundos. Qual é a velocidade dessa onda?
a) 12,5 m/s, no sentido negativo do eixo x;
b) 1,25 m/s, no sentido negativo do eixo x;
c) 1,25 m/s, no sentido positivo do eixo x;
d) 25 m/s, no sentido positivo do eixo x;
e) 0,25 m/s, no sentido negativo do eixo x;
Ver solução completaQuestão 41
Um dado ponto em uma corda por onde passa uma onda senoidal apresenta menor velocidade quando
o módulo do deslocamento é máximo
o módulo da aceleração é máximo
o módulo do deslocamento é mínimo
o módulo do deslocamento é metade da amplitude
o módulo do deslocamento é um quarto da amplitude
Ver solução completaQuestão 42
Se uma onda senoidal transversal com uma amplitude de e uma frequência de está se propagando em uma corda, a velocidade máxima de qualquer ponto da corda é:
- 4,0 m/s
- Não há dados suficientes para responder.
Questão 43
Uma massa ligada a uma mola tem posição instantânea , com em centímetros e em segundos. A velocidade da massa é a metade da sua velocidade inicial no instante:
Questão 44
O deslocamento de uma corda na qual existe uma onda transversal é dado por , onde é uma função e é uma constante positiva. Qual das afirmações abaixo não é necessariamente verdadeira?
- A forma da onda não muda enquanto se propaga ao longo da corda;
- A forma da corda no instante é dada por ;
- A velocidade da onda é ;
- A frequência da onda é ;
- A onda se propaga no sentido positivo do eixo ;
Questão 45
Uma certa onda transversal é descrita por:
A velocidade de propagação desta onda vale:
Questão 46
Qual das seguintes alternativas é certa para a função:
Onde x e y estão dados em metros quando t é expressado em segundos?
(a) y(x, t) representa uma onda progressiva que em 6 s percorre uma distancia de 8 m.
(b) y(x, t) representa uma onda progressiva com uma velocidade de propagação de 4 m/s.
(c) y(x, t) representa uma onda progressiva que se movimenta no sentido positivo do eixo x.
(d) y(x, t) não representa uma onda progressiva.
(e) y(x, t) representa uma onda progressiva tranversal onde o máximo deslocamento vertical é 0,5 m.
Ver solução completaQuestão 47
Durante um intervalo de tempo de exatamente um período de vibração de um diapasão, o som emitido percorre uma distância:
A) igual ao comprimento do diapasão
B) igual a duas vezes o comprimento do diapasão
C) de cerca de
D) de dois comprimentos de onda no ar
E) de um comprimento de onda no ar
Ver solução completaQuestão 48
Considere uma onda transversal que se propaga no eixo e é dada pela equação
.
O gráfico abaixo apresenta o instantâneo do deslocamento (em ) em função da posição (em ) no instante . Já o gráfico apresenta o deslocamento (em ) em função do tempo (em ) para . Expressando suas respostas no sistema internacional de unidades (SI), determine:
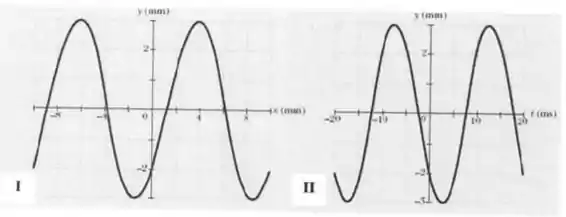
- A amplitude e o número de onda .
- O período e a frequência angular .
- A constante de fase .
Questão 49
A figura mostra o deslocamento de uma onda progressiva em uma determinada posição como função do tempo e o deslocamento da mesma onda em um dado momento como função da posição. Determine o comprimento de onda dessa onda.
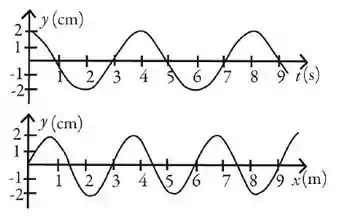
- 2,0 cm
- 3,0 m
- 2,0 m
- 4,0 m
- 1,5 cm
Questão 50
A gráfico abaixo mostra o deslocamento do equilíbrio de uma onda transversal nos instantes (linha tracejada) e (linha contínua). Durante este intervalo o máximo que estava em cm moveu-se para . A frequência das oscilações desta onda vale:
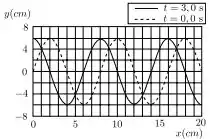
(a)
(b)
(c)
(d)
Ver solução completaQuestão 51
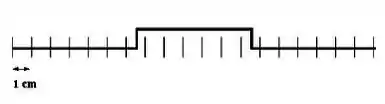
Dois pulsos estão viajando um em direção ao outro a 10 cm/s em uma corda longa em t = 0 s, como mostrado ao lado. Qual o diagrama abaixo mostra corretamente a forma da corda em 0,5 s?
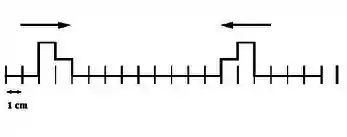
A)
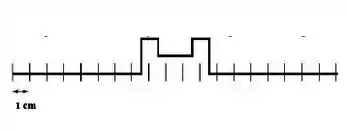
B)
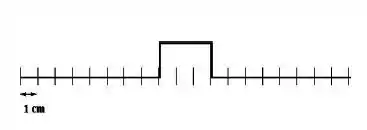
C)
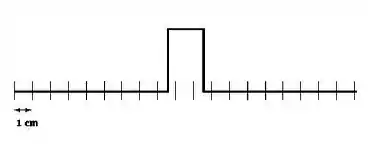
D)
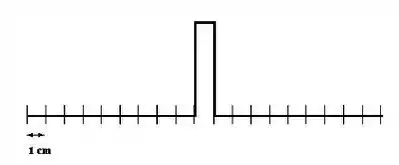
E)
Questão 52
Um dado ponto em uma corda por onde passa uma onda senoidal apresenta maior velocidade quando:
- O modulo do deslocamento é mínimo
- O modulo do deslocamento é um quarto da amplitude.
- O modulo da aceleração é máximo.
- O modulo do deslocamento é máximo.
- O modulo do deslocamento é metade da amplitude
Questão 53
A figura abaixo apresenta a evolução temporal de um ponto, de uma onda senoidal propagando-se a no sentido positivo.
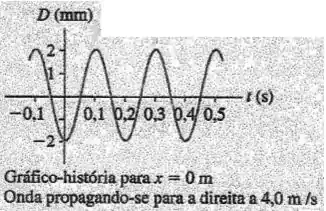
Qual o comprimento de onda correspondente?
Qual é a constante de fase de onda?
Escreva a equação para os deslocamentos produzidos no meio por essa onda (em função do tempo e do espaço)
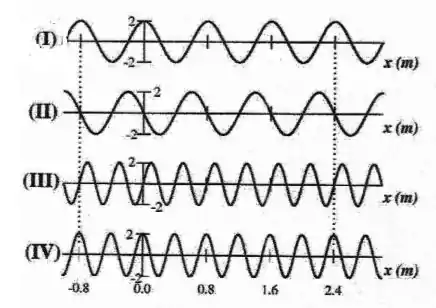
Qual das figuras ou abaixo, representa a imagem da onda para o instante
Questão 54
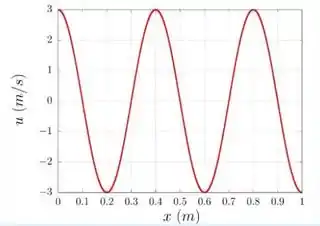
. Na figura estamos mostrando o gráfico da velocidade transversal dos pontos de uma corda na qual se propaga uma onda. O gráfico está em um estante de tempo fixo, em que é a posição do elemento da corda. Dado que a velocidade de propagação nessa corda é de , encontre a amplitude e a frequência .
. e
. e
. e
. e
. e
Ver solução completaQuestão 55
Uma corda tem massa e comprimento . Ela vibra, com as duas extremidades fixas, num modo normal descrito pela função de onda:
com em metros e em segundos. Determine:
- O comprimento de onda desta onda.
- O número de ventres e a posição de ventre.
- A frequência de vibração de cada ponto da corda.
- A tensão a qual a corda está submetida.
- Determine o comprimento de onda do próximo modo normal de vibração com frequência mais alta.
Questão 56
Uma corda de um violão feita de aço está sob uma tração de . O diâmetro da corda é de e o comprimento, quando tracionada, é de . Determine o comprimento desta corda quando não tracionada. .
Ver solução completaQuestão 57
A figura abaixo mostra o perfil de uma onda transversal que se propaga com velocidade no sentido crescente de .
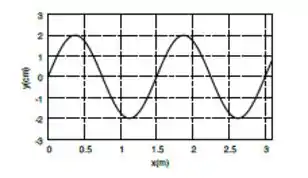
- Qual o comprimento de onda desta onda?
- Qual o período das oscilações de um dado ponto?
- Usando a forma de função de onda ), com , para descrever esta onda, determine .(Dica: Pelo gráfico vê-se que a velocidade do ponto na origem é negativa em .)
- Qual a velocidade máxima atingida por um ponto qualquer?
Justifique suas respostas.
Ver solução completaQuestão 58
(Cap 13 - Ex 1) A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um lá uma oitava acima que é igual a duas vezes a frequência da corda do piano.
Ver solução completaQuestão 59
(Cap 13 - Ex 2) Se um objeto sobre uma superfície horizontal, sem atrito, é preso a uma mola, deslocado e depois libertado, ele irá oscilar. Se ele for deslocado 0,120 m da sua posição de equilíbrio e libertado com velocidade inicial igual a zero, depois de 0,800 s verifica-se que o seu deslocamento é de 0,120 m no lado oposto e que ele ultrapassou uma vez a posição de equilíbrio durante esse intervalo. Ache (a) a amplitude, (b) o período, (c) a frequência.
Ver solução completaQuestão 60
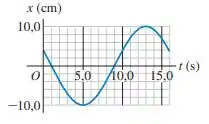
(Cap 13 - Ex 4) O deslocamento de um objeto oscilando em função do tempo é mostrado na Figura 13.30. Quais são (a) a frequência; (b) a amplitude; (c) o período; (d) a frequência angular desse movimento?
Questão 61
Ao longo de uma corda de tamanho com ambas as extremidades fixas, propagam-se ondas de modo a formar uma onda resultante que obedece à expressão:
(c) No eixo fornecido a seguir, faça um esboço dessa onda no instante
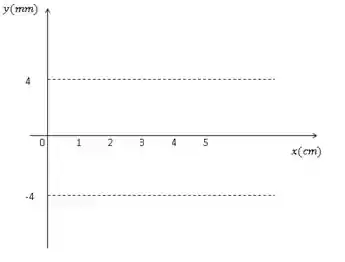
d) Encontre a expressão da velocidade transversal da onda e calcule seu valor, para o instante, nos pontos , e .
Ver solução completaQuestão 62
Uma onda progressiva se propaga para a direita em uma corda esticada como mostrado na figura abaixo. A imagem mostra uma foto instantânea do pulso em um certo instante de tempo. Os pontos A, B e C são pontos que representam partículas da corda. Qual opção abaixo corretamente descreve como as partículas na corda estão se movendo entre A e B, e entre B e C?
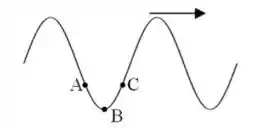

Questão 63
(Cap 15- Ex 8) Uma onda se desloca na água em linha reta sobre um lago é descrita pela equação
Onde y é o deslocamento perpendicular à superfície sem perturbações do lado. a) Quanto tempo leva para que uma configuração completa de onda passe por uma pescador em um barco ancorado, e que distancia horizontal a crista da onda percorre nesse tempo? b) Qual é o numero da onda e o numero de ondas por segundo que passam pelo pescador? c) Com que velocidade uma crista de onda se desloca ao passar pelo pescador?, e qual a velocidade máxima de seu flutuador de cortiça quando a onda o faz oscilar para cima e para baixo?
Ver solução completaQuestão 64
(Cap 15- Ex 6) Uma certa onda transversal é descrita por
Determine para esta onda a) a amplitude; b) o comprimento de onda; c) a frequência; d) a velocidade de propagação; e) a direção de propagação.
Ver solução completaQuestão 65
(Cap. 15. Problemas Desafiadores - Ex.82)Um escafandrista está suspenso abaixo da superfície do Lago Ness por um cabo preso a um barco na superfície do lago (Figura 15.40). O mergulhador e seus equipamentos possuem massa total de e ocupam um volume igual a . O cabo possui diâmetro igual a e a densidade linear . O mergulhador imagina que viu algo se movendo nas profundezas escuras do lago e sacode a extremidade do cabo , produzindo ondas transversais que sobem através do cabo para sinalizar a seus companheiros que estão no barco.
a) Qual é a tensão no cabo em sua extremidade inferior presa ao mergulhador? Não se esqueça de incluir a força de empuxo que a água (densidade igual a ) exerce sobre ele.
b) Calcule a tensão no cabo a uma distância acima do mergulhador. A força de empuxo que a água exerce sobre o cabo deve ser incluída.
c) A velocidade de propagação de uma transversal é dada por equação (15.13). Portanto, a velocidade varia ao longo do cabo, visto que a tensão não é constante. (Esta relação despreza a força de amortecimento que a água exerce sobre o cabo que se move.) Integre para achar o tempo que o primeiro sinal leva para atingir a superfície.
Ver solução completaQuestão 66
(Cap 15 - Ex 9) Quais das seguintes funções satisfazem a função de onda dada pela Equação (15.2)? a) ; b) ; c) ; d) Para a onda do item (b), escreva a equação para a velocidade transversal e a aceleração transversal de uma partícula no ponto x.
Ver solução completaQuestão 67
(Cap 15 - Ex 11) Uma onda senoidal propaga-se ao longo de uma corda esticada sobre o eixo . O deslocamento da corda em função do tempo é indicado na figura 15.30 para partículas nos pontos e .
- Qual é a amplitude da onda?
- Qual é o período da onda?
- Informamos a você que a distância entre os pontos e é menor do que o comprimento de onda. Determine a velocidade e o comprimento de onda quando ela se propaga no sentido .
- Supondo agora que a onda se propague no sentido , determine a velocidade e o comprimento de onda.
- Seria possível determinar de forma não ambígua o comprimento de onda calculado dos itens e se você não usasse o dado de a distância entre os pontos ser menor do que o comprimento de onda? Justifique sua resposta.
Questão 68
(Cap.16.2 – Ex.6) Um grande terremoto com epicentro em Loma Pietra, na Califórnia, perto de São Francisco, ocorreu às da tarde, hora local, no dia de outubro de (em TUC, Tempo Universal Coordenado, ocorreu à no dia de outubro de ). As ondas sísmicas primárias (ondas ) de um terremoto são ondas longitudinais que se propagam na crosta terrestre. Ondas desse terremoto foram detectadas em Caracas, na Venezuela, à , TUC; em Kevo, na Finlândia, à , TUC; e em Viena, Áustria, à , TUC. As distâncias percorridas pelas ondas desde o epicentro em Loma Pietra foram de até Caracas, até Kevo e até Viena.
- Use os tempos de chegada das ondas para calcular a velocidade média de propagação das ondas até essas três cidades. Como você explica eventuais diferenças entre essas velocidades médias?
- A densidade média da crosta terrestre é igual a aproximadamente . Use esse valor para calcular o módulo de compressão da crosta terrestre ao longo da trajetória seguida pelas ondas até elas atingirem cada uma das três cidades. Como suas respostas se comparam com os módulos de compressão listados na tabela 11.1?
Questão 69
. Numa corda de comprimento , propaga-se uma onda com a seguinte função de onda:
Quais os gráficos da posição da corda nos instantes e .
.
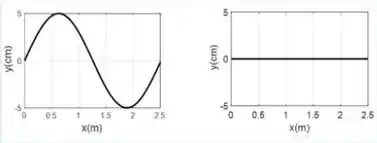
.
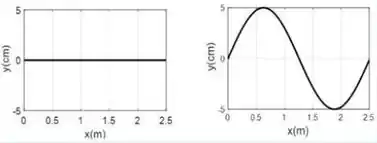
.
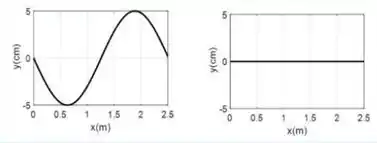
.
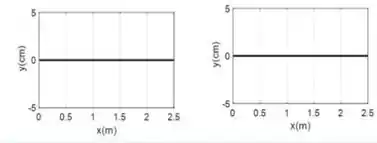
.
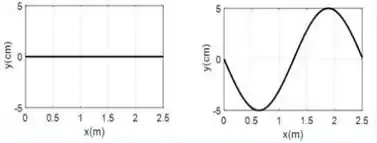
Questão 70
Um dispositivo vibrador com frequência de 50 Hz em contato com a água produz ondas circulares atingem uma parede 100s após terem sido originadas no vibrador. Sabendo-se que o comprimento de onda apresentado foi de 20cm, determine a distância do objeto vibrador a parede.
- 500 m.
- 5.000 m.
- 200 m.
- 1.000 m.
- 2.000 m.
Questão 71
. Uma onda senoidal se propaga no sentido positivo do eixo-. Na figura estamos fornecendo a densidade de energia cinética por comprimento de uma corda no instante , onde é a posição do elemento de corda. Essa quantidade é definida como (onde o termo elevado ao quadrado, , é a velocidade transversal da onda na corda) e sua unidade é . A frequência da onda é de . Utilizando as informações do gráfico, encontre:
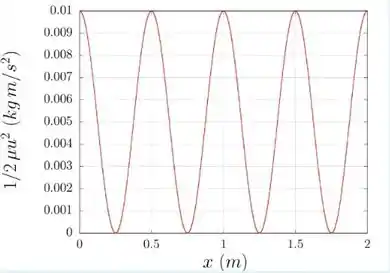
O comprimento de onda e o número de onda .
Se a tração for de , encontre a massa específica linear da corda.
Encontre a amplitude da onda e escreva para essa corda.
Ver solução completaQuestão 72
A figura ao lado representa uma onda senoidal em um dado instante de tempo que se propaga da esquerda para direita em uma corda muito longa. Marque a alternativa que mostra as direções e sentidos das velocidades dos elementos de corda posicionados nos pontos A, B, C e D:
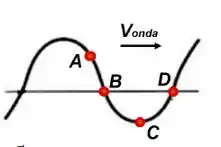
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 73
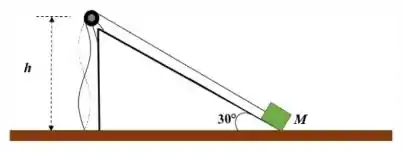
Na figura abaixo podemos verificar um plano inclinado, tanto a polia como o plano inclinado não têm atrito. A corda de comprimento total suporta um bloco de massa . Através da figura é possível notar, que o bloco de massa está na base do plano, a corda tem uma massa total , e o sistema está em equilíbrio. Considere que a massa da corda é pequena em relação à massa do bloco, note na figura, que a parte vertical da corda tem um comprimento e somente nesta região são formadas as ondas estacionárias. A aceleração da gravidade é .
- Determine a velocidade das ondas na corda.
- Determine o (comprimento de onda) da onda estacionária no segundo harmônico.
Escolha uma:
- Nenhuma das alternativas
Questão 74
O deslocamento vertical de uma corda transportando uma onda senoidal viajando é dado por:
onda é a amplitude da onda, o número de onda e a frequência. No tempo , o ponto em tem um deslocamento e está se movendo na direção positiva. A constante de fase é:
Questão 75
Qual das afirmações abaixo a respeito das ondas é FALSA?
- Uma onda transporta energia de um ponto para outro.
- Uma onda é uma perturbação que se propaga de um ponto para outro.
- A perturbação das partículas de um meio pode ser em uma direção perpendicular à direção de propagação da onda.
- As ondas sonoras são longitudinais.
- Uma onda transporta as partículas de um meio de um ponto para outro.
Questão 76
Para a onda mostrada na figura ao lado, o comprimento de onda é:
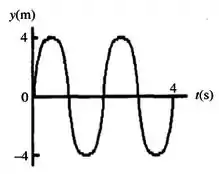
A) 8 m.
B) 4 m.
C) 2 m.
D) 1 m.
E) impossível determinar com as informações fornecidas na figura.
Ver solução completaQuestão 77
Uma onda periódica se propaga através de uma corda na direção mostrada na figura abaixo. Essa imagem mostra uma fotografia da onda em um certo instante de tempo. Os pontos indicados A, B e C são pontos sobre a corda. Qual opção abaixo descreve corretamente como as partículas da corda entre A e B e entre B e C estão se movendo?
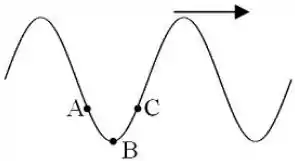
entre A e B entre B e C
A) para baixo para baixo
B) para cima para baixo
C) para a esquerda para a direita
D) para cima para cima
E) para baixo para cima
Ver solução completaQuestão 78
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
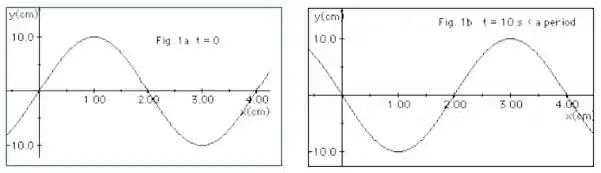
c. Em que instante posterior ocorrerá outra crista na posição ?
Ver solução completaQuestão 79
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
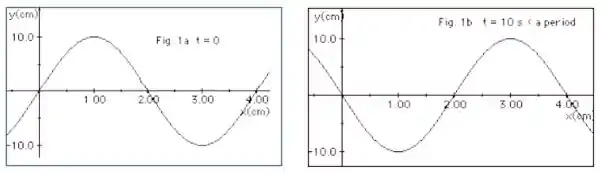
b. Nesse tempo , determine, à direita no eixo x, as duas próximas posições onde ocorrerão cristas.
Ver solução completaQuestão 80
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
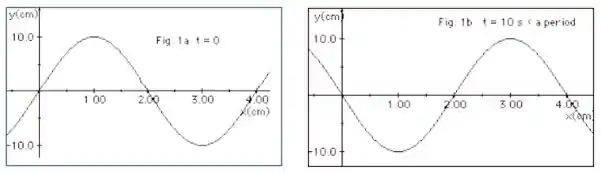
e. O número de cristas que passam em x = 1,0 cm no tempo de 80 s.
Ver solução completaQuestão 81
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
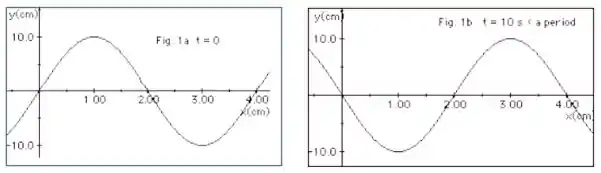
h. Escreva uma função que seja apropriada para descrever o deslocamento y dos pontos da corda para quaisquer valores de x e de t.
Ver solução completaQuestão 82
No instante a amplitude de uma onda transversal que propaga na direção de com velocidade é dada pelo gráfico abaixo. No sistema a equação que descreve a onda é:
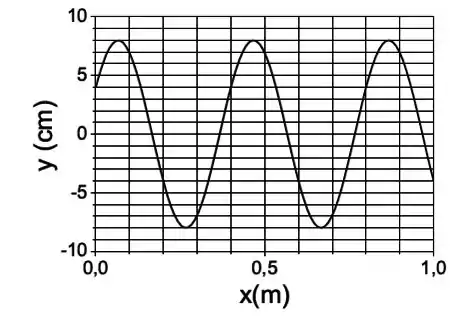
a)
b)
c)
d)
e)
Ver solução completaQuestão 83
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
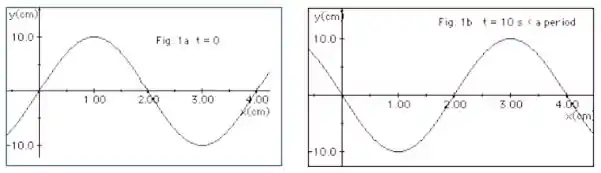
a. O comprimento de onda, a frequência e a velocidade da onda.
Ver solução completaQuestão 84
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
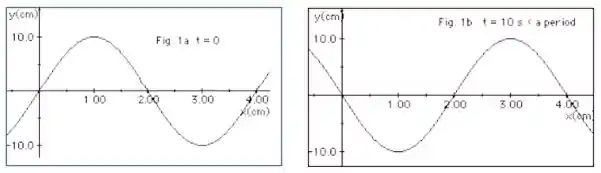
d. O número de vezes, no tempo de um período, que o deslocamento da corda é nulo na posição x = 2,0 cm.
Ver solução completaQuestão 85
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
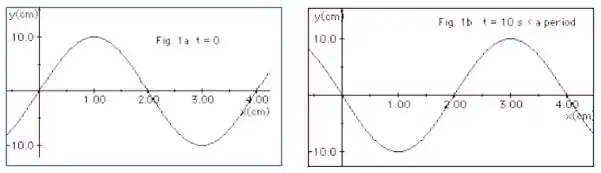
f. Desenhe, em um gráfico, o comportamento do deslocamento y em função do tempo para as posições x = 0, x = 2 cm e x = 4,0 cm, para o intervalo de t = 0 até t= 20 s.
Ver solução completaQuestão 86
A Figura 1a (abaixo) representa uma onda em t =0 se deslocando-se para a direita ao longo de uma corda. Já na Figura 1b a mesma onda está representada mas, em um tempo t = 10 s, sendo esse tempo uma fração do período T da onda. Com essas informações determine:
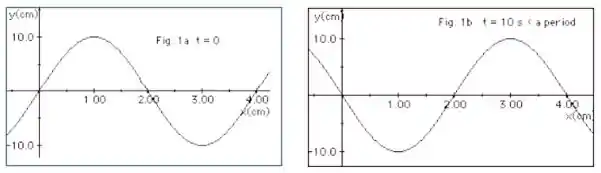
g. O ponto x = 0 da corda está em fase com os pontos x = 2,0 cm e x = 4,0 cm? Explique.
Ver solução completaQuestão 87
A figura abaixo mostra o gráfico-instantâneo e o gráfico-história para um pulso de onda que se propaga em uma corda esticada. Os gráficos descrevem a onda sob diferentes perspectivas. Qual o sentido de propagação da onda e sua velocidade?

a) sentido negativo de x, 2 m/s
b) sentido negativo de x, 3 m/s
c) sentido negativo de x, 4 m/s
d) sentido positivo de x, 2 m/s
e) sentido positivo de x, 4 m/s
Ver solução completaQuestão 88
Os pontos frios de um forno de micro-ondas estão separados por 6,0cm. Qual é a frequência das micro-ondas nesse caso?
Ver solução completa
Questão 89
Duas canoas estão separadas por 10m na superfície de um lago, na qual ondas se propagam. Cada canoa oscila periodicamente para cima e para baixo, indo do seu ponto mais alto para o mais baixo e retornando ao início em 8,0 segundos. Quando uma canoa está no seu ponto de maior altura, a outra está no seu ponto mais baixo, e todos os pontos entre elas estão a alturas intermediárias. Determine a velocidade das ondas no lago.
A) 1,25 m/s
B) 5,0 m/s
C) 2,5 m/s
D) 0,63 m/s
E) 0,75 m/s
Ver solução completaQuestão 90
O sol a estrela mais próxima da terra, é constituído principalmente de gás hidrogênio e hélio, os dois gases mais leves que temos. Recebemos dessa estrela, radiação, luz vermelha, luz azul, raios gama e raios x. E possível afirmar que todas essas radiações têm em comum, no vácuo.
- nada em comum.
- comprimento de onda.
- frequência.
- a amplitude de onda.
- a velocidade de propagação.
Questão 91
O desenho abaixo mostra a imagem, em um determinado instante fixo no tempo, de uma onda que se propaga em uma corda esticada no sentido indicado pela seta. Observe os pontos A,B e C da corda.
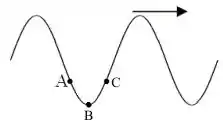
Qual das opções abaixo descreve corretamente em que direções os pontos da corda nos intervalos entre A e B e entre B e C estão se movendo neste instante?
Entre A e B Entre B e C
A) para baixo para cima
B) para cima para cima
C) para a direita para a direita
D) para baixo para baixo
E) para cima para baixo
Ver solução completaQuestão 92
O deslocamento de uma corda vibrante em função da posição num certo instante é mostrado na figura. A onda viaja na direção positiva do eixo x com velocidade de 10 cm/s. A e B são dois pontos da corda. Determine (a) a frequência da onda e (b) a diferença de fase entre o ponto B e o potno A.
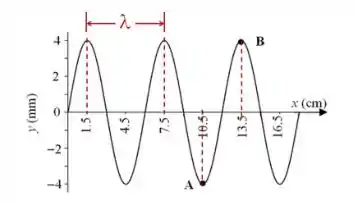
Questão 93
João e Maria estão boiando no mar, separados por uma distância de 5,0 m, quando uma lancha passa nas proximidades. Com a passagem da lancha, o casal começa a oscilar para cima e para baixo com uma frequência de 0,25 Hz. No instante em que Maria passa pelo ponto mais alto da oscilação, João está passando pelo ponto mais baixo. Se a distância entre João e Maria é menor que um comprimento de onda, qual é a velocidade das ondas produzidas pela
lancha?
a) 1,3 m/s;
b) 2,5 m/s;
c) 3,8 m/s;
d) 5,0 m/s;
e) 7,5 m/s;
Ver solução completaQuestão 94
Uma onda sonora senoidal é descrita pelo deslocamento . Determine o comprimento de onda, velocidade dessa onda e a velocidade máxima do movimento oscilatório de um elemento.
Escolha uma:
- Nenhuma das alternativas
Questão 95
Uma onda transversal em uma corda é descrita pela seguinte expressão:
![]()
Na expressão acima, y(x,t) e x são dados em metros, e t em segundos. Qual das seguintes afirmações sobre essa onda é falsa?
- A onda está viajando no sentido negativo do eixo x.
- A amplitude da onda é de 1,0 m.
- A frequência da onda é de 0,10 Hz
- O comprimento de onda é de 2,0 m.
- A velocidade da onda é de 5,0 m/s.
Questão 96
Em 20 segundos, uma fonte de ondas periódicas emite 40 ondas completas, que se propagam com comprimento de onda de 15 m. Determine o período, a frequência e a velocidade da onda.
Ver solução completaQuestão 97
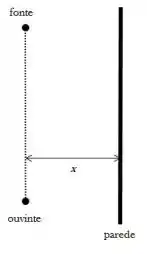
Uma fonte sonora emite um som que se propaga até uma ouvinte localizada a uma certa distância . Uma parede, paralela à reta ligando fonte e ouvinte, se encontra a uma certa distância de ambos (ver figura). A parede reflete o som, e a onda sonora refletida chega à ouvinte e interfere com o som que vem diretamente da fonte. A ouvinte não ouvirá som algum apenas se:
- As distâncias e forem iguais.
- A distância for um número inteiro de comprimentos de onda.
- A distância for um número ímpar de meio comprimentos de onda.
- A distância for um número inteiro de comprimentos de onda.
- A distância for um número ímpar de meio comprimentos de onda.
Questão 98
Uma corda tem uma extremidade presa a uma parede. Você segura a extremidade livre esticando a corda, e em seguida balança a corda gerando uma onda progressiva. Se de repente você começar a balançar a corda mais rapidamente sem mudar apreciavelmente a tensão, podemos afirmar que:
- a velocidade da onda aumenta e sua frequência se mantém constante.
- a velocidade da onda se mantém constante e sua frequência aumenta.
- a velocidade da onda se mantém constante e a frequência se mantém constante.
- a velocidade da onda diminui e a frequência aumenta.
- a velocidade da onda aumenta e sua frequência aumenta.
Questão 99
Uma onda senoidal é produzida numa corda que está esticada ao longo do eixo . O deslocamento da corda em função do tempo está representado na figura para partículas na posição e .
- Qual é a amplitude da onda?
- Qual é o período da onda?
- Escreva a equação da onda em função de e assumindo que a onda está se propagando no sentido . Use para o número de onda. Atenção para a fase! [Dica: use os pontos e para achar a fase.]
- Se os pontos m estão contidos em um intervalo de um comprimento de onda e assumindo que a onda se propaga no sentido , determine o comprimento de onda e a velocidade da onda.
Se necessário use