Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 14.Exercícios e Problemas - Ex. 7
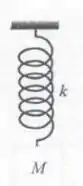
14.7E A) Mostre que a lagrangeana do oscilador visto na Figura 14.7 é , onde é o ponto de referência para a energia potencial gravitacional. B) Mostre que o bloco oscila com frequência angular em torno do ponto de coordenada .
Passo 1
Belezoca galerinha, a lagrangeana do sistema é dada por:
Onde é a energia cinética do sistema, enquanto é a energia potencial. E como se trata de um sistema massa mola na vertical, temos que a energia cinética é dada por:
E como estamos nos deslocando em , temos que o deslocamento é e sua derivada representará a velocidade , tal que:
Passo 2
Já a energia potencial, é formada por energia potencial da mola e energia potencial gravitacional devido ao deslocamento , tal que:
Dessa maneira a lagrangeana é:
E como o bloco possui massa , a mola possui constante elástica e o sistema oscila harmonicamente, vamos ter que: