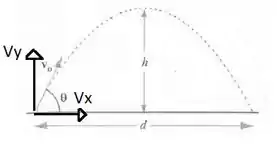
A Figura 5.13 mostra um projétil sendo atirado com velocidade inicial , a qual faz um ângulo com a horizontal. O projétil move-se sem atrito sob a ação da gravidade até cair novamente no solo. Calcule: A) a altura máxima atingida pelo projétil; B) a distância atingida.

Certo, agora quero que percebam uma coisa. Quando o projétil estiver na altura máxima, ele não vai mais subir, em outras palavras a componente é igual a , quando a altura é máxima.

Vocês lembram da equação de Toricelli? Ela é dada por:

Vamos aplica ela na componente . Logo,

Note que a aceleração do corpo é a gravidade e como ela está contraria ao movimento (puxando para baixo), vamos ter um sinal de negativo na equação.

Como já sabemos que, , vamos obter que

Lembra-se do passo 1, onde decompomos o vetor , então, temos que:

Aplicando na , temos

Para obtermos a distância, ou seja, na componente , devemos nos atentar que diferente da componente , trata-se de um movimento uniforme. Em outras palavras, não tem aceleração.

Logo, lembre-se que

Com isso, temos:

Mas certo! E como vamos descobrir o tempo total que a partícula executa o movimento? E se eu disser que já temos o tempo de subida? Acredita?

Vamos lá! Olhando novamente para componente , a aceleração desenvolvida (gravitacional) pode ser representado como:

Substituindo,

E como,

Substituindo na equação da componente , vamos obter que

Assim,