Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.1 - Ex. 12
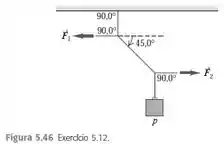
Na Figura , o peso é igual a .
a) Qual é a tensão na corda diagonal?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado pediu pra gente calcular (a) a tensão na corda diagonal do sistema e (b) os módulos das forças horizontais e que devem ser exercidas para manter em equilíbrio esse sistema.
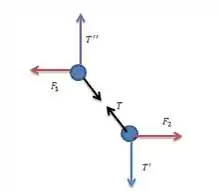
Antes de qualquer coisa nesse tipo de questão mesmo que não seja pedido pra fazer um diagrama de corpo livre é importante fazer mesmo assim! Assim ficam mais claro quais forças se equilibram! Saca só:
Aqui eu chamei de as tensões nas cordas e as bolinhas representam os nós no fio. Como o sistema está em equilíbrio, cada nó tem força resultante zero.
Daí analisando cada nó e equacionando as forças vamos encontrar um sistema de equações e resolver para encontrar cada uma das forças.
Vamos lá!
Passo 2
Você vai ver que não é um bicho de sete cabeças! Dá uma olhada lá no desenho e compara o peso com a força .
Elas não se equilibram? Sim! Pois é, então já temos que .
Agora olhando para o mesmo ponto, mas agora para o nó, temos:
A primeira equação é o equilíbrio das forças na direção vertical! Assim podemos determinar a tensão :
Show!
Passo 3
Agora vamos olhar para o mesmo nó, mas agora na direção horizontal! Saca só:
E daqui conseguimos determinar o valor da primeira força fazendo:
Beleza! Agora vamos analisar o outro nó para descobrir a outra força!
Passo 4
Para o nó de cima temos:
Da equação de cima vamos descobrir a segunda força:
Que é igual ao valor de !!
Valeu, galera! Até a próxima! 😉