Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 14.1 - Ex. 7
Em 1654, Otto Von Guericke, o inventor da bomba de vácuo, fez uma demonstração para os nobres do Sacro Império Romano na qual duas juntas de oito cavalos não puderam separar dois hemisférios de cobre evacuados. (a) Supondo que os hemisférios tinham paredes finas (mas resistentes), de modo que (Figura) pode ser considerado tanto o raio interno como o raio externo, mostre que o módulo da força necessária para separar os hemisférios é dada por , onde é a diferença entre a pressão do lado de fora e a pressão do lado de dentro da esfera. (b) Supondo que , e e determine o módulo da força que as juntas de cavalos teriam que exercer para separar os hemisférios. (c) Explique por que uma única junta de cavalos poderia executar a mesma demonstração se um dos hemisférios estivesse preso em uma parede.
Passo 1
- Primeiramente, vamos analisar apenas um dos hemisférios:
- De posse do resultado anterior, podemos facilmente determinar o valor da força necessária quando , e . Sabendo que :
- Caso um dos hemisférios estivesse preso a uma parede e o outro puxado por cavalos, teríamos o diagrama de forças representado na figura abaixo
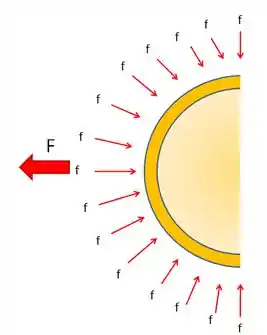
Imagine que a casca esféfica é subdividida em várias pequenas unidades de área. A pressão atmosférica externa à esfera exerce, em cada uma dessas áreas que compõem os hemisférios , uma pequena força de magnitude .
Vamos dar um “zoom” na superfície esférica e analisar uma dessas unidades de área.
Passo 2
Para calcularmos a magnitude da força horizontal necessária para separar os hemisférios, precisamos determinar o somatório das componentes horizontais das pequeninas forças , representadas por . Analisando o “zoom” aplicado em uma unidade infinitesimal de área de acordo com a figura, podemos perceber que
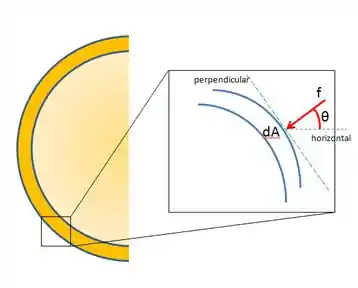
Lembrando que é o ângulo formado entre a linha de ação da força f (que passa pelo centro da esfera) e a horizontal.
Passo 3
Agora, precisamos saber como determinar a área de um componente de superfície como o demonstrado acima. Na figura abaixo, temos uma “fatia” horizontal de uma esfera no lado esquerdo, e, no lado direito, podemos observar a projeção transversal de um quarto de esfera.
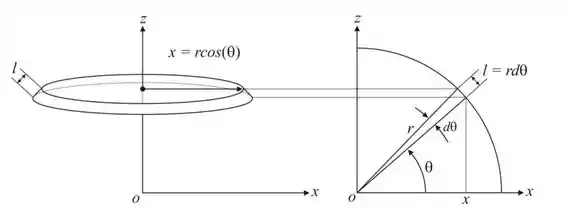
Podemos considerar que, dando um zoom sobre um elemento de área de esfera, ele pode ser considerado como um retângulo de comprimento e altura .
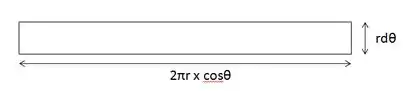
Logo, é fácil ver que a área superficial da esfera pode ser subdividida em áreas de magnitude, que variam com o ângulo apresentado na figura da seguinte forma:
Passo 4
Agora que possuímos o valor das áreas em função do ângulo, podemos determinar as componentes horizontais de força que a pressão atmosférica exerce sobre cada elemento de área.
Para obtermos o valor da força horizontal necessária para separar os hemisférios, precisamos somar essas componentes de força por meio da seguinte integração:
Lembre-se que o ângulo varia de a , de acordo com a figura acima. Realizando a integração, chegamos ao resultado pedido.
Passo 5
Passo 6
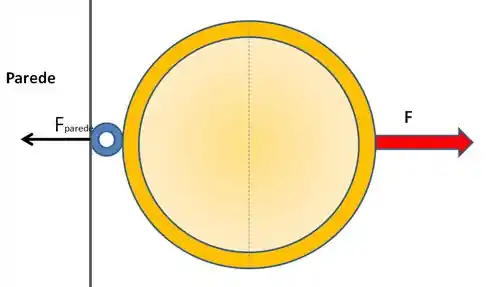
Nesse caso, o equilíbrio de forças externas atuantes na horizontal garante que a força resultante exercida sobre o hemisfério direito pelos cavalos e a força exercida pela parede sobre o hemisfério esquerdo sejam iguais. Logo, como a força exercida pela parede é igual à exercida pelos cavalos, podemos perceber que apenas uma junta de cavalos poderia ser utilizada para executar a mesma demonstração.
Resposta
(b)