Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 76
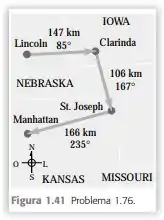
1.76 - Em um vôo de treinamento, uma aprendiz de piloto voa de Lincoln, no Estado de Nebraska, até Clarinda, no Iowa; a seguir até St. Joseph, no Missouri; depois até Manhattan, no Kansas (Figura 1.41). Os ângulos formados pelos deslocamentos são medidos em relação ao norte: 0° significa o sentido do sul para o norte, 90° é o leste, 180° é o sul e 270° é o oeste. Use o método dos componentes para achar a) a distância que ela terá de voar para voltar para Lincoln; b) a direção (em relação ao norte) que ela deverá voar para voltar ao ponto de partida. Ilustre a solução fazendo um diagrama vetorial.
Passo 1
Vamos chamar o trajeto de Lincoln até Clarinda de , de Clarinda até St. Joseph (famoso São José) de , de St. Joseph até Manhattan de e de Manhattan até Lincoln de .
Quando o avião for de Manhattan até Lincoln, o trajeto vai fechar. Isso significa que a soma dos trajetos vai ser igual a 0. Agora fazer essa questão ficou fácil! É só somar todas as trajetórias em x e em y e igualar a 0, daí encontramos das componentes de , depois é só fazer Pitágoras pra achar o módulo de D e usar a tangente pra encontrar o ângulo.
Então simbora!
Passo 2
Como os ângulos estão relacionados ao sentido norte, a direção norte-sul será o nosso y e a direção leste-oeste o nosso x.
Vamos, agora, decompor as trajetórias em x:
Agora em y:
Passo 3
Agora a gente vai usar o maravilhoso Teorema de Pitágoras pra encontrar o módulo de :
Achamos a distância!!!
Partiu letra (b)!
Passo 4
Pra achar a direção com relação ao eixo norte vamos usar a tangente do ângulo, mas antes vamos desenhá-lo para ter certeza que estamos fazendo certo:
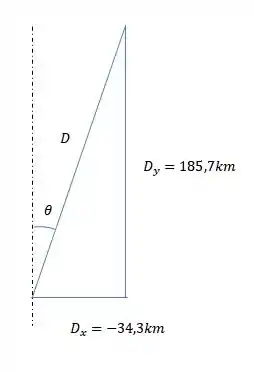
Repara que o ângulo que desejamos encontrar nesse caso é com a vertical (com o Norte conforme dito no enunciado).
Vamos fazer isso através da tangente.
Agora tiramos o arco-tangente desse valor pra encontrar o ângulo:
Passo 5
Agora o nosso lindo diagrama:
Terminamos a questão!! É pra comemorar, aluno do Responde Aí!
Resposta
- 189km
- 10,2° em relação ao norte.