Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 1.1 - Ex. 77
Um trenó em repouso é subitamente puxado em três direções horizontais ao mesmo tempo, mas não vai a lugar algum. Paul puxa para o nordeste com uma força de . Jhonny puxa a um ângulo de a sul do oeste com uma força de . Connie puxa com uma força a ser determinada. (a) expresse as duas forças dos garotos em termos dos vetores unitários usuais. (b) Determine a terceira força (a feita por Connie), expressando-a primeiro na forma das componentes e então como uma magnitude e um ângulo (direção).
Passo 1
(a) Vamos fazer um desenho que represente as duas forças conhecidas:
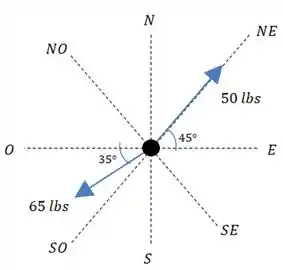
Ao dizer que temos uma força com um ângulo de a sul do oeste, o enunciado quis dizer que o ângulo sai da linha do oeste e vai em direção ao sul, como a gente desenhou.
Vamos dizer que aponta para e aponta para , então os vetores são:
Percebe que a segunda força só tem componentes negativas porque elas aponta para o sentido negativo de e .
Agora vamos calcular esses valores numéricos:
Como nossos dados iniciais não tinham casa decimal, nossos resultados também não terão.
Passo 2
(b) Vamos escrever a força exercida por Connie na forma vetorial, com os vetores unitários
Para descobrir qual é a terceira força só temos que lembrar do fato de que o trenó está em repouso. Isso quer dizer que a força resultante deve ser zero
Isso implica em
Substituindo as componentes das nossas forças, ficamos com um sistema:
E então a terceira força tem a seguinte forma:
Passo 3
(b) E agora vamos escrever essa mesma força como uma magnitude e um ângulo. Primeiro calculamos a magnitude:
Como os dois valores são positivos, sabemos que está no “primeiro quadrante” do nosso sistema.
Se o ângulo que esse vetor forma com o eixo horizontal - é , nós podemos calculá-lo da seguinte forma:
E então é um vetor de magnitude igual a formando um ângulo de no sentido anti-horário a partir do eixo horizontal.
Resposta
(a) e .
(b) O terceiro vetor é , com magnitude e formando anti-horário com a horizontal.