Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 88
O vetor possui comprimento de 3,50 cm e aponta para o interior desta página. O vetor aponta do canto direito inferior desta página para o canto esquerdo superior desta página. Defina um sistema apropriado de coordenadas com orientação da mão direita e ache os três componentes do produto vetorial medidos em cm². Faça um diagrama mostrando o sistema de coordenadas e os vetores .
Passo 1
E aí, pessoal!
Nesse problema foram descritos dois vetores e nosso objetivo é obter o produto vetorial entre eles...
Parece complicado?
Pra achar as três componentes vamos usar a equação 1.27 do livro que nos diz quais as componentes do produto vetorial:
.
Veja só!
Passo 2
Se aponta pro interior da página, quer dizer que ele é perpendicular a ela, então ele não tem a componente x e y. Por causa disso o seu módulo depende só de z e é -3,50cm, porque está para dentro e não para fora do plano.
A página tem 20cm de largura por 35cm de comprimento, como o vetor compreende toda a página, suas componentes são exatamente as dimensões da página. Então temos:
Tranquilo até aqui? 😬
Passo 3
Agora falta usar a fórmula do módulo em para acha-lo:
Bacana, não é?
Passo 4
Como todas as componentes de C dão 0 pela equação 1.27, não temos um vetor no produto vetorial.
Então chegou a grande hora de fazer o determinante pra achar as componentes do produto vetorial. Vem comigo!
A partir do determinante, sabemos que:
E encontramos as componentes! \o/
Passo 5
Agora chegou a hora de fazer os diagramas. Começando por :
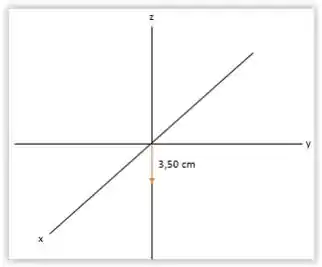
Agora o :
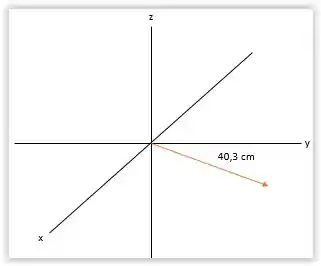
E por último, mas não menos importante, o vertor :
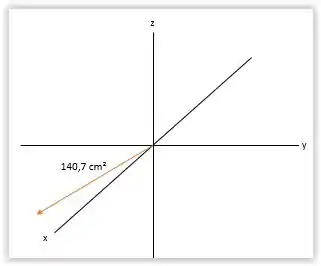
E finalmente acabamos!!
E aí! o que achou? Responde Aí! 😎