Uma formiga-de-fogo, em busca de molho picante em uma área de piquenique, executa três deslocamentos sucessivos no nível do solo: , de para sudoeste (ou seja, entre sul e oeste), , de m para leste, e , de em uma direção ao norte do leste. Suponha que o sentido positivo do eixo aponte para leste e o sentido positivo do eixo para o norte. Quais são (a) a componente e (b) a componente de ? Quais são (c) a componente e (d) a componente de ? Quais são (e) a componente e (f) a componente de ?
Passo 1
Vamos representar um vetor de apontando na direção sudoeste:
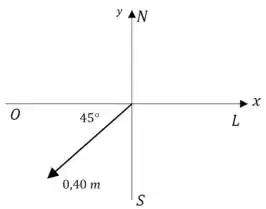
(a) Nesse caso, a componente é:
(b) E a componente é:
Passo 2
Agora vamos representar um vetor de apontando na direção leste:

(c) Nesse caso, a componente é:
(d) E a componente é:
Passo 3
Por último. vamos representar um vetor de apontando em uma direção ao norte do leste:

(e) Nesse caso, a componente é:
(f) E a componente é:
Passo 4
Agora que já calculamos todas as componentes de cada um dos deslocamentos, vamos escrever , e em forma vetorial:
Podemos usar isso para calcular o deslocamento total:
(g) Então a componente do deslocamento total é .
(h) A componente do deslocamento total é .
Passo 5
(i) Agora que já conhecemos o vetor do deslocamento total , podemos calcular o seu módulo:
E como as duas componentes do vetor são positivas, sabemos que ele aponta para algum lugar no primeiro quadrante.
Então podemos definir totalmente a sua orientação se calcularmos o ângulo que ele forma com o eixo :
Ou seja, ao norte do leste.
Passo 6
(k) Para que a formiga volte diretamente para o ponto de partida, ela precisará andar uma distância igual ao módulo do deslocamento total:
(l) E como o deslocamento apontava ao norte do leste, para voltar ao ponto de partida a formiga deve andar ao sul do leste.
Resposta
(a) A componente de é .
(b) A componente de é .
(c) A componente de é .
(d) A componente de é zero.
(e) A componente de é .
(f) A componente de é .
(g) A componente do deslocamento total é .
(h) A componente do deslocamento total é .
(i) O módulo do deslocamento total é .
(j) O sentido do deslocamento total é ao norte do leste.
(k) A formiga deve percorrer .
(l) Ela deve ser mover ao sul do leste.